2���������̉��̔z�u�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
2���������F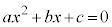 ��2���Ɋւ����������Aa�Cb�Cc�Ɋւ�����������߂��肪����܂��B
��2���Ɋւ����������Aa�Cb�Cc�Ɋւ�����������߂��肪����܂��B
2���������̉��ƌW���̊W��p���ĊȒP�ɉ����ł���ꍇ������܂����A�����̏ꍇ�͉����̂��̂����Ă����ƔώG�ɂȂ�₷���̂ł��B
���������ꍇ�ɂ́A�ȉ��Ɏ����悤�ȃO���t�ɒ��ڂ���Z�I��m���Ă���ƕ֗��ł�(�Ȃ��A2���������̈�ʘ_�Q��)�B
2���������F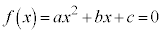 (
(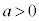 ) ����@ ��2��������α�Cβ?(
) ����@ ��2��������α�Cβ?(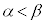 )���Ƃ��܂��B
)���Ƃ��܂��B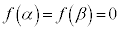 �ł��B
�ł��B
���̂Ƃ��A�@�̔��ʎ��F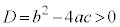 ����A ���������܂��B
����A ���������܂��B
 �܂��A2���������Ƃ���γ�����傫����A
�܂��A2���������Ƃ���γ�����傫����A �̃O���t�̎��F
�̃O���t�̎��F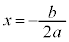 �́A
�́A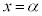 ��
��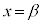 �̊Ԃɗ���̂ŁA���̈ʒu�ɂ��Ă��A
�̊Ԃɗ���̂ŁA���̈ʒu�ɂ��Ă��A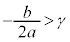 ����B �����藧���܂��B
����B �����藧���܂��B
�������Ȃ���A�A�ƇB�����ł͕s�\���ł��B
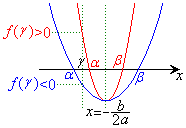
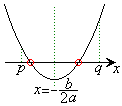
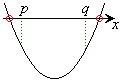
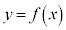 �̃O���t���E�}�̐��̂悤�ɂȂ��Ă��܂��ꍇ�A�O���t��x���Ƃ̌�_�̂��������̂��̂̈ʒu������ƁA
�̃O���t���E�}�̐��̂悤�ɂȂ��Ă��܂��ꍇ�A�O���t��x���Ƃ̌�_�̂��������̂��̂̈ʒu������ƁA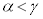 �ɂȂ��Ă��܂��B
�ɂȂ��Ă��܂��B
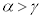 �ƂȂ邽�߂ɂ́A�E�}�̐Ԑ��̂悤�ɁA
�ƂȂ邽�߂ɂ́A�E�}�̐Ԑ��̂悤�ɁA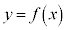 �̃O���t��
�̃O���t��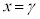 �̈ʒu�ɂ����ẮA����x���̏㑤��ʉ߂��Ă��Ȃ���Ȃ�܂���B
�̈ʒu�ɂ����ẮA����x���̏㑤��ʉ߂��Ă��Ȃ���Ȃ�܂���B
�܂�A���̑��ݔ͈͂̒[�_�ɂ���������F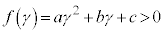 ����C �Ƃ����������K�v�ł��B
����C �Ƃ����������K�v�ł��B
�t�ɁA�A���B���C�����藧�Ƃ��ɁA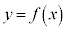 �̃O���t��x����
�̃O���t��x����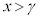 �̕����Ō����̂ŁA�@��2�������͂Ƃ���γ�����傫���Ȃ�܂��B
�̕����Ō����̂ŁA�@��2�������͂Ƃ���γ�����傫���Ȃ�܂��B
�ȏ�̂悤�ɁA2���������̉��Ɋւ���������A�u���ʎ��A���̈ʒu�A�[�_�̊��l�v��3�̏������������邱�Ƃɂ��l�@���邱�Ƃ��ł��܂��B
2���������̉��̔z�u�̖��ł́A�u���ʎ��A���̈ʒu�A�[�_�̊��l�v���l����Ɗo���Ă����Ă��������B
 2���������F
2���������F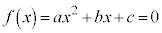 (
(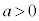 )��2���������Ƃ���
)��2���������Ƃ���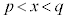 �͈̔͂ɑ��݂�����������߂�Ƃ��ɂ́A
�͈̔͂ɑ��݂�����������߂�Ƃ��ɂ́A
�E�}���A
���ʎ��F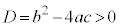
���̈ʒu�F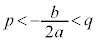
�[�_�̊��l�F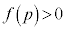 ����
����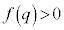
���l���邱�ƂɂȂ�܂��B
 �ގ��̖��ŁA
�ގ��̖��ŁA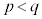 ���Ƃ��āA2���������F
���Ƃ��āA2���������F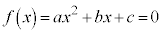 (
(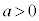 )�̈���̉���
)�̈���̉���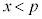 �C�����̉���
�C�����̉���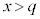 �ɑ��݂�����������߂�Ƃ��ɂ́A�h
�ɑ��݂�����������߂�Ƃ��ɂ́A�h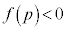 ����
����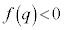 �h���l���邾���ł��݂܂��B���ʎ��Ǝ��̈ʒu���m�F����K�v�͂���܂���B
�h���l���邾���ł��݂܂��B���ʎ��Ǝ��̈ʒu���m�F����K�v�͂���܂���B
�Ȃ��Ȃ�A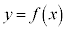 �̃O���t�́A
�̃O���t�́A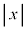 ���ǂ�ǂ�傫�����Ă����ƁAx������ꡂ��ɏ���̕��ւƐL�тĂ����܂��B
���ǂ�ǂ�傫�����Ă����ƁAx������ꡂ��ɏ���̕��ւƐL�тĂ����܂��B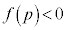 �ł���A
�ł���A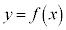 �̃O���t��
�̃O���t��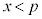 �̕�����x���ƌ����܂��B�܂��A
�̕�����x���ƌ����܂��B�܂��A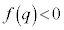 �ł���A
�ł���A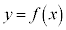 �̃O���t��
�̃O���t��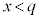 �̕�����x���ƌ����܂��B�܂�A
�̕�����x���ƌ����܂��B�܂�A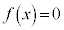 �̈���̉���
�̈���̉���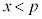 �C�����̉���
�C�����̉���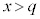 �ɑ��݂��܂��B
�ɑ��݂��܂��B
 ��D2���������F
��D2���������F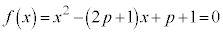 ���l����B
���l����B
(1) ���قȂ�2�����Ƃ���1����ł���Ƃ��A����p�Ɋւ�����������߂�B
(2) 1����1��菬�����A1����3���傫���Ƃ��A����p�Ɋւ�����������߂�B
(3) ���قȂ�2�����Ƃ���0�����傫��1�����������Ƃ��A����p�Ɋւ�����������߂�B
(1) ���ʎ��F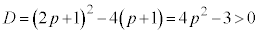 ���A
���A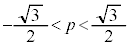 ����@
����@
���F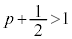 ���A
���A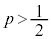 ����A
����A
�[�_�̊��l�F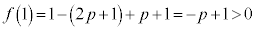 ���A
���A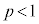 �@����B
�@����B
�@���A���B���A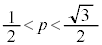 .......[��]
.......[��]
(2) 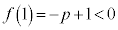 ���A
���A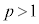 ����C
����C
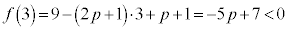 ���A
���A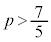 ����D
����D
�C���D���A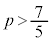 ......[��]
......[��]
(3) ���ʎ��F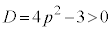 ���A
���A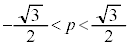 ����E
����E
���F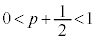 ���A
���A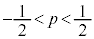 ����F
����F
�[�_�̊��l�F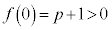 ����
����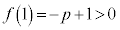 ���A
���A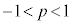 ����G
����G
�E���F���G���A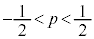 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B