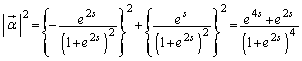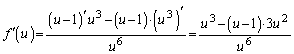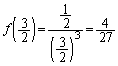��嗝�n���w'09�N�O��[5]
�Ȑ�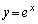 ����_P�̎���t�ɂ�������W��
����_P�̎���t�ɂ�������W��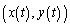 �ƕ\���AP�̑��x�x�N�g���Ɖ����x�x�N�g�������ꂼ��
�ƕ\���AP�̑��x�x�N�g���Ɖ����x�x�N�g�������ꂼ��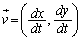 ��
��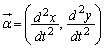 �Ƃ���B���ׂĂ̎���t��
�Ƃ���B���ׂĂ̎���t��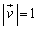 ����
����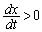 �ł���Ƃ��āA���̖₢�ɓ�����B
�ł���Ƃ��āA���̖₢�ɓ�����B
(1) P���_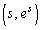 ��ʉ߂��鎞���ɂ����鑬�x�x�N�g��
��ʉ߂��鎞���ɂ����鑬�x�x�N�g��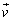 ��s��p���ĕ\���B
��s��p���ĕ\���B (2) P���_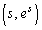 ��ʉ߂��鎞���ɂ���������x�x�N�g��
��ʉ߂��鎞���ɂ���������x�x�N�g��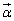 ��s��p���ĕ\���B
��s��p���ĕ\���B (3) P���Ȑ��S�̂��Ƃ��A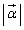 �̍ő�l�����߂�B
�̍ő�l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�P�ɔ������Ă��������̖��ł����A�Ȑ��̎����^�����Ă��āA���_��x���W�Ay���W������t�̊��Ƃ��ė^�����Ă��Ȃ��̂ŁA�������̔����@�̗��p���l���邱�ƂɂȂ�܂��B
(1) �Ȑ��F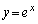 �@����@
�@����@ y��x�Ŕ�������ƁA
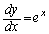 �@����A
�@����A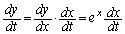 �@����B
�@����B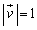 ���A
���A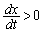 ���A
���A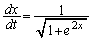 �@����C
�@����C�B���A
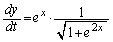 �@����D
�@����DP���_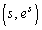 ��ʉ߂��鎞���ɂ����鑬�x�x�N�g��
��ʉ߂��鎞���ɂ����鑬�x�x�N�g��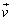 �́A
�́A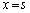 �Ƃ��āA
�Ƃ��āA 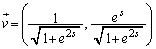 ......[��]
......[��]
(2) �����x�x�N�g����x�����́A
�ł����A�C�ł�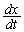 ��x�̊��ŗ^�����Ă��āAt�̊��̌`�����Ă��Ȃ��̂ŁA�������̔����@��p���܂��B
��x�̊��ŗ^�����Ă��āAt�̊��̌`�����Ă��Ȃ��̂ŁA�������̔����@��p���܂��B �����x�x�N�g����y�����A
�����l�ɁA�D�ł�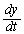 ��x�̊��ŗ^�����Ă���̂ŁA�������̔����@��p���܂��B
��x�̊��ŗ^�����Ă���̂ŁA�������̔����@��p���܂��B P���_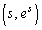 ��ʉ߂��鎞���ɂ���������x�x�N�g��
��ʉ߂��鎞���ɂ���������x�x�N�g��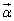 �́A
�́A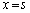 �Ƃ��āA
�Ƃ��āA 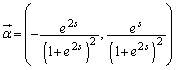 ......[��]
......[��]
(3) P���Ȑ��S�̂��Ƃ��A(2)��s�͑S�������Ƃ�܂��B
���̂܂�s�̊��ƌ���s�Ŕ������Ă��悢�̂ł����A�v�Z�����N�ɂ��邽�߂ɁA
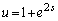 (
(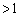 )
)�Ƃ�����u�̊��ƌ��邱�Ƃɂ��܂�(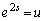 �Ƃ��Ȃ��̂́A������ł��邾���ȒP�ɂ��邽��)�B
�Ƃ��Ȃ��̂́A������ł��邾���ȒP�ɂ��邽��)�B ���A
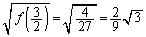 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
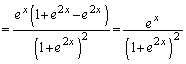
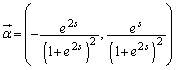 ......[��]
......[��]