��嗝�n���w'09�N���[4]
�_Q�͎��̋K���Ő�������̕��łȂ������̏�𐳂̕����֓������̂Ƃ���B������n�͕��łȂ������Ƃ���B
(a) ����0�ł͓_Q�͌��_�ɂ���B
(b) �_Q������T�ō��W �ɂ���Ƃ��A����
�ɂ���Ƃ��A����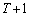 �ɂ͊m��
�ɂ͊m�� �ō��W
�ō��W �ֈړ����A�m��
�ֈړ����A�m��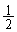 �ō��W
�ō��W �ֈړ�����B
�ֈړ�����B (c) �_Q������T�ō��W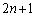 �ɂ���Ƃ��A����
�ɂ���Ƃ��A����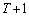 �ɂ͊m��1�ō��W
�ɂ͊m��1�ō��W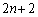 �ֈړ�����B
�ֈړ�����B �_Q������T�ō��Wj�ɂ���m���� �Ə������Ƃɂ���B�ȉ��̖₢�ɓ�����B
�Ə������Ƃɂ���B�ȉ��̖₢�ɓ�����B
(1) ���ׂĂ̎��R��j�ɑ��� �����߂�B
�����߂�B (2) T�Cj�����R���ł���Ƃ��A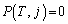 �ƂȂ������T�Cj��p���ĕ\���B
�ƂȂ������T�Cj��p���ĕ\���B (3) T�����R���ł���Ƃ�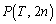 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ӊO�Ǝ苭���m���̖��ł��B�_Q�̓������ǂ����Ă������A�Ƃ������ƂŁA�����ɂ���Ă͓��ɂȂ��Ă��܂��܂��B���ɁA���`�}��`���đQ�����𗧂Ă悤�Ƃ���ƓD���ɂ͂܂邩���m��܂���B
�����ł́A�ȉ��̂悤�ɋL���̕��ו��ōl���邱�Ƃɂ��܂��B
����T���玞�� �ւ̓_Q�̓����ɂ�3�ʂ肠���āA
�ւ̓_Q�̓����ɂ�3�ʂ肠���āA
�E���W ������W
������W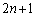 �ւ̈ړ�(�m��
�ւ̈ړ�(�m��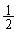 �C���ŕ\���܂�)
�C���ŕ\���܂�) �E���W ������W
������W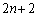 �ւ̈ړ�(�m��
�ւ̈ړ�(�m�� �C���ŕ\���܂�)
�C���ŕ\���܂�) �E���W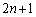 ������W
������W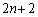 �ւ̈ړ�(�m��1�C�~�ŕ\���܂�)
�ւ̈ړ�(�m��1�C�~�ŕ\���܂�) �̂����ꂩ���J��Ԃ����̂ŁA���Ɓ��Ɓ~�̕��ѕ����l���邱�Ƃɂ��܂��B
(a)���A�ŏ��́������ł��B
(b)�C(c)���A���ɂ����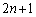 �ֈړ�����̂ŁA�ŏI��Ɂ��ŏI������ꍇ�������ā��̎��ɂ͕K���~�����܂��B�܂��~�ɂ����
�ֈړ�����̂ŁA�ŏI��Ɂ��ŏI������ꍇ�������ā��̎��ɂ͕K���~�����܂��B�܂��~�ɂ���� �ֈړ�����̂ŁA�~��2��ȏ㑱�����Ƃ͂���܂���B�@���(��)
�ֈړ�����̂ŁA�~��2��ȏ㑱�����Ƃ͂���܂���B�@���(��)
�Ȍ�A
0��2��4��5�~6��8
�̂悤�ɁA����T�ɂ�������W�Ǝ���T���玞��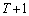 �ւ̈ړ����������C���C�~���A�_Q�̑��݈ʒu�̍��W�ƌ��݂ɏ����悤�ɂ��܂��B
�ւ̈ړ����������C���C�~���A�_Q�̑��݈ʒu�̍��W�ƌ��݂ɏ����悤�ɂ��܂��B
�܂��A���Ɓ~�̏o������m�Ƃ���ƁA��(�o������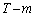 )�ł͍��W��2�i�݁A�����邢�́~�ł͍��W��1�i�ނ̂ŁA����T�܂łɎ�����W�́A
)�ł͍��W��2�i�݁A�����邢�́~�ł͍��W��1�i�ނ̂ŁA����T�܂łɎ�����W�́A
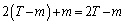 �@����@
�@����@
(1)  �͎���2�܂ł̈ړ��̊m���Ȃ̂ŁA���Ɓ��Ɓ~�̂����ꂩ��2���ׂ邱�ƂɂȂ�܂��B
�͎���2�܂ł̈ړ��̊m���Ȃ̂ŁA���Ɓ��Ɓ~�̂����ꂩ��2���ׂ邱�ƂɂȂ�܂��B 0��2��4�@�m���́A 0��2��3�@�m���́A
0��2��3�@�m���́A 0��1�~2�@�m���́A
0��1�~2�@�m���́A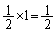
����ȊO�̏ꍇ�͂���܂���B����āA
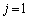 �C
�C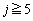 �̂Ƃ�
�̂Ƃ� �C
�C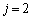 �̂Ƃ�
�̂Ƃ�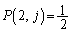 �C
�C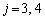 �̂Ƃ�
�̂Ƃ� ......[��]
......[��]
(2) ����T�܂łɎ�����Wj���ő�ɂȂ�̂́A����T�܂ł̈ړ������ׂā��̂Ƃ��ŁA�e������2�����W�������āA �܂ŗ��܂��B����āA
�܂ŗ��܂��B����āA �ƂȂ邱�Ƃ͂Ȃ��A
�ƂȂ邱�Ƃ͂Ȃ��A �̂Ƃ�
�̂Ƃ�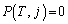 �ł��B
�ł��B ����T�܂łɎ�����Wj���ŏ��ɂȂ�̂́A����T�܂ł̈ړ��������~�����ɂȂ�Ƃ��ŁA�e������1�����W�������āA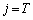 �܂ŗ��܂��B����āA
�܂ŗ��܂��B����āA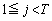 �ƂȂ邱�Ƃ͂Ȃ��A
�ƂȂ邱�Ƃ͂Ȃ��A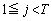 �̂Ƃ�
�̂Ƃ�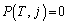 �ł��Bj��
�ł��Bj�� �������R���̂Ƃ��A(��)�ɒ��ӂ��āA���Ɓ~�̌�m���A
�������R���̂Ƃ��A(��)�ɒ��ӂ��āA���Ɓ~�̌�m���A �ł���A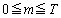 �ł����āA�@���A����T�Ɏ�����W��j�ƂȂ�̂ŁA
�ł����āA�@���A����T�Ɏ�����W��j�ƂȂ�̂ŁA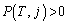 �ł��B
�ł��B
����āA���߂�����́A  �܂���
�܂���  ......[��]
......[��]
(3) ����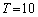 �܂łŋN���肤��S�Ă̏ꍇ�������o���Ă݂܂��B
�܂łŋN���肤��S�Ă̏ꍇ�������o���Ă݂܂��B 0��2��4��6��8��10
0��2��4��6��8��9
0��2��4��6��7�~8
0��2��4��5�~6��8
0��2��3�~4��6��8
0��1�~2��4��6��8
0��2��4��5�~6��7
0��2��3�~4��6��7
0��1�~2��4��6��7
0��2��3�~4��5�~6
0��1�~2��4��5�~6
0��1�~2��3�~4��6
0��1�~2��3�~4��5
�����̍��W�Ɏ���Ƃ��A�Ō�̈ړ��́����~�ŁA���ɂ͂Ȃ�܂���B
���W10�Ɏ���Ƃ��́A�S�ā��ŁA�m����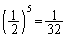
���W8�Ɏ���Ƃ��́A����3��A���~�̑�����1��ŁA�m����
���W6�Ɏ���Ƃ��́A����1��A���~�̑�����2��ŁA�m����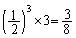
������AT�����R���ł���Ƃ��A����T�܂łɁ��~�̑����̉�m�́A �����A���~�̑����̉�m�̂Ƃ�(�����̍��W�Ɏ���Ƃ��A�Ō�̈ړ������ɂȂ邱�Ƃ͂Ȃ��̂ŁA�K�����~�̑����Ō���܂�)�A����
�����A���~�̑����̉�m�̂Ƃ�(�����̍��W�Ɏ���Ƃ��A�Ō�̈ړ������ɂȂ邱�Ƃ͂Ȃ��̂ŁA�K�����~�̑����Ō���܂�)�A����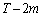 ��ŁA����T�܂łɎ�����W
��ŁA����T�܂łɎ�����W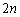 �́A
�́A ��  ���̂Ƃ��A
���̂Ƃ��A ���A
���A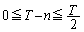 �C
�C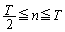 �C����āA����T�܂łɎ�����W
�C����āA����T�܂łɎ�����W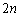 �ɂ��āA
�ɂ��āA ����T�܂ł̕��т̒��ɁA���Ɓ��� ��܂��B
��܂��B
�܂��A���~�̑�����1�g�Ƃ��Č���ƁA���Ɓe���~'���킹��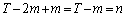 �̕��ו��́A
�̕��ו��́A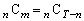 �ʂ肠��܂�(�g�ݍ��킹���Q��)�B
�ʂ肠��܂�(�g�ݍ��킹���Q��)�B
�� 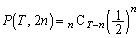 �@(
�@( �̎w����n�́��Ɓ��̏o���ł�)
�̎w����n�́��Ɓ��̏o���ł�)
(2)���A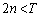 �C
�C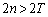 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A �ł��B
�ł��B
��  ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ......[��]
......[��]