��嗝�n���w'09�N���[5]
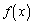 ��
��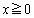 �Œ�`���ꂽ�A���Ȋ��Ƃ��Aa�Cb�𐳂̒萔�Ƃ���B���̂Ƃ��A
�Œ�`���ꂽ�A���Ȋ��Ƃ��Aa�Cb�𐳂̒萔�Ƃ���B���̂Ƃ��A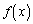 ��
��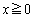 ��
��
�̊W�������̂Ƃ���B�ȉ��̖₢�ɓ�����B
(1) 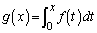 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A ���������邱�Ƃ������B
(2) 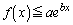 ���������邱�Ƃ������B
���������邱�Ƃ������B (3) 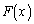 ��x�ɂ��ĘA���Ȋ��ŁA�C�ӂ̓�̎���α�Cβ �ɑ��āA���̊W�������̂Ƃ���B
��x�ɂ��ĘA���Ȋ��ŁA�C�ӂ̓�̎���α�Cβ �ɑ��āA���̊W�������̂Ƃ���B ����ɁA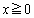 �Œ�`���ꂽ��̘A���Ȋ�
�Œ�`���ꂽ��̘A���Ȋ�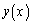 ��
��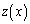 �͎��̊W���������̂Ƃ���B
�͎��̊W���������̂Ƃ���B 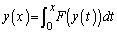 �C
�C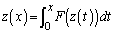
���̂Ƃ��A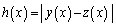 �Ƃ����A
�Ƃ����A ���������邱�Ƃ������B
(4) 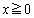 ��
��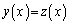 �ł��邱�Ƃ��ؖ�����B
�ł��邱�Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ۓI�Ȗ��Ƃ��������łȂ��A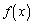 �C
�C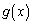 �C
�C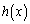 �C
�C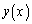 �C
�C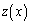 �ƁA���낢��Ȋ��̐ϕ���������炪�o�Ă���̂ŁA�ڈڂ肵�ĂȂ��Ȃ��œ_����܂�ɂ������ł��B�����������́A�Ƃɂ���������āA���낢�뎎�s���낷��ׂ��ł��B
�ƁA���낢��Ȋ��̐ϕ���������炪�o�Ă���̂ŁA�ڈڂ肵�ĂȂ��Ȃ��œ_����܂�ɂ������ł��B�����������́A�Ƃɂ���������āA���낢�뎎�s���낷��ׂ��ł��B
(3)�ł́A��ϕ��Ɋւ��鐫���𗘗p����̂ł����A�����ł́A�����Ƃ����ɁA�ؖ������݂܂��B
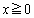 �C
�C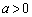 �C
�C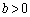 �Ƃ��āA
�Ƃ��āA
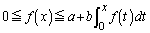 �@����@
�@����@
���A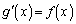 �C�����p���āA
�C�����p���āA �@���A
�����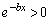 ���A
���A
(2) �Ȃ��Ȃ��肪����̂��߂Ȃ����ł����A�����ׂ��s�����F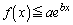 �̉E�ӂƇ@�̉E�ӂ��r���Ă݂܂��B
�̉E�ӂƇ@�̉E�ӂ��r���Ă݂܂��B ���ꂪ�A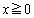 �ɂ�����0�ȏ�ƂȂ邱�Ƃ�������Γs���������̂ł����A(1)������ƁA
�ɂ�����0�ȏ�ƂȂ邱�Ƃ�������Γs���������̂ł����A(1)������ƁA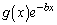 �Ƃ����`��������̂ŁA
�Ƃ����`��������̂ŁA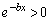 ���A
���A 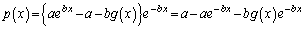 �@����B
�@����B�Ƃ����āA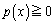 ���������Ƃ�ڕW�ɂ��܂��B(1)�̌��ʂ�p���āA
���������Ƃ�ڕW�ɂ��܂��B(1)�̌��ʂ�p���āA ������A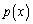 ��
��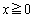 �ɂ����ĒP�������ł���A�A��
�ɂ����ĒP�������ł���A�A��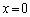 �Ƃ�����
�Ƃ�����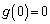 �ƂȂ�̂ŁA�B���(���̑������Q��)�A
�ƂȂ�̂ŁA�B���(���̑������Q��)�A ����āA�@��p���āA
(3) 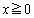 �Ƃ��āA
�Ƃ��āA 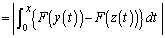 �@����C
�@����C��蕶���̊W���F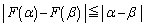 �ɂ����āA
�ɂ����āA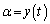 �C
�C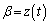 �Ƃ���ƁA
�Ƃ���ƁA 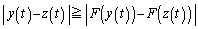 (
(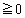 )
)����āA
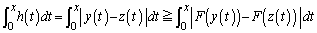 �@����D
�@����D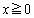 �Œ�`���ꂽ�A���Ȋ�
�Œ�`���ꂽ�A���Ȋ�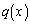 �ɂ��āA
�ɂ��āA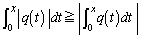 �@����E
�@����E�ƂȂ�̂ŁA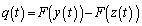 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A ����ƁA�C�C�D���A
���D�E�͊��m�Ƃ��Ă��悢�̂ł����A�ؖ����Ă����܂��B
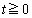 �ɂ����āA�˂�
�ɂ����āA�˂�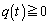 �ł���Ƃ��ɂ́A
�ł���Ƃ��ɂ́A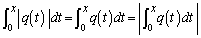 �@����F
�@����F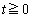 �ɂ����āA�˂�
�ɂ����āA�˂�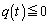 �ł���Ƃ��ɂ́A
�ł���Ƃ��ɂ́A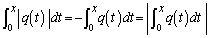 �@����G
�@����G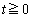 �ɂ����āA
�ɂ����āA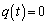 ����t��n�����āA
����t��n�����āA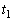 �C
�C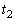 �C����C
�C����C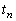 �Ƃ��܂��B�܂��A
�Ƃ��܂��B�܂��A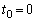 �C
�C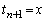 �Ƃ��܂��B
�Ƃ��܂��B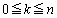 �ƂȂ鐮��k�ɂ��āA
�ƂȂ鐮��k�ɂ��āA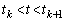 �̂Ƃ�
�̂Ƃ�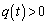 �ł���A
�ł���A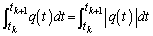 (
(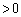 )
)�ł����A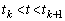 �̂Ƃ�
�̂Ƃ�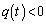 �ł���A
�ł���A �]���āA
�� 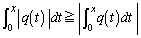 �ȏ���F�C�G���܂߂āA�E���������܂��B
�ȏ���F�C�G���܂߂āA�E���������܂��B
(4) (3)�̌��ʂ�����ƁA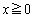 �ɂ����Ē�`���ꂽ�A���Ȋ�
�ɂ����Ē�`���ꂽ�A���Ȋ�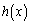 �ɂ��āA�@�ŁA
�ɂ��āA�@�ŁA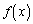 ��
��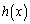 �Ƃ��A
�Ƃ��A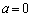 �C
�C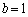 �Ƃ����s���������藧�̂ŁA(2)�̌��ʂŁA
�Ƃ����s���������藧�̂ŁA(2)�̌��ʂŁA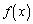 ��
��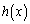 �Ƃ��A
�Ƃ��A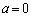 �C
�C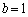 �Ƃ����s���������藧���܂��B����āA
�Ƃ����s���������藧���܂��B����āA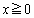 �ɂ����āA
�ɂ����āA �� 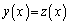 �@(�ؖ��I)
�@(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B