東北大理系数学'09年後期[2]
アメ玉の入った缶がある。白のアメ玉が11個、赤黄緑青の4色のアメ玉がそれぞれ1個ずつ、合計15個入っている。缶の中身をよく混ぜてから3個同時に取り出す。取り出した3個について以下の確率と期待値を求めよ。
(1) 3個とも白のアメ玉である確率。
(2) 緑のアメ玉が含まれる確率。
(3) 緑と青のアメ玉の個数の合計の期待値。
(4) 白以外のアメ玉の個数の期待値。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 確率、期待値に関する基本問題です。(3)では、15個中に緑玉と青玉は2個あるので、3個取り出せば、そのうちの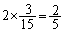
個が緑と青の個数の合計の期待値になりそうです。(4)では、白以外の玉は4個あるので、3個取り出せば、そのうちの
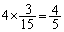個が白以外の個数の期待値になりそうです。
(1) 全事象は、15個のアメ玉から3個を選ぶので、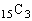
通り(組み合わせを参照)。 取り出した3個とも白になる場合の数は、11個の白玉から3個を選ぶので、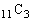
通り。
求める確率は、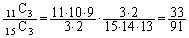 
......[答]
(2) 取り出した3個の中に緑のアメ玉が含まれる場合の数は、取り出した3個のうち1個は緑玉で確定し、緑以外の14個から残り2個を選ぶので、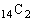
通り。 求める確率は、
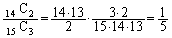......[答]
(3) 取り出した3個の中に緑と青がともに含まれる場合の数は、取り出した3個のうち2個は緑玉と青玉で確定し、緑と青以外の13個から残り1個を選ぶので、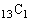
通り。 緑と青で2個になる確率は、
取り出した3個の中に緑が含まれ青が含まれない場合の数は、取り出した3個のうち1個は緑玉で確定し、緑と青以外の13個から残り2個を選ぶので、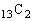
通り(青が含まれ緑が含まれないときも同様)。
緑と青で1個になる確率は、 求める期待値は、
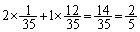......[答]
(4) 取り出した3個が3個とも白以外になる場合の数は、白以外の4個から3個を選ぶので、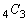
通り。この確率は、 取り出した3個のうち2個が白以外になる場合の数は、白以外の4個から2個を選ぶのが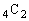
通り、白11個から残る1個を選ぶのが
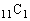通りで、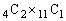
通り。白以外が2個になる確率は、 取り出した3個のうち1個が白以外になる場合の数は、白以外の4個から1個を選ぶのが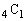
通り、白11個から残る2個を選ぶのが
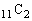通りで、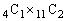
通り。白以外が1個になる確率は、 求める期待値は、
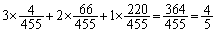......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
