�}�g�吔�w'09�N[3]
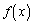 �𐮎��ŕ\�������Ƃ��A
�𐮎��ŕ\�������Ƃ��A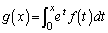 �Ƃ����B�C�ӂ̎���x�ɂ���
�Ƃ����B�C�ӂ̎���x�ɂ���
�����藧�Ƃ���B
(1) 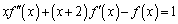 �����藧���Ƃ������B
�����藧���Ƃ������B (2) 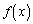 �͒萔�܂���1�����ł��邱�Ƃ������B
�͒萔�܂���1�����ł��邱�Ƃ������B (3) 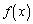 �����
�����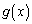 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�A�������������̂悤�Ɍ����܂����A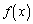 �͐����A�Ƃ����w�肪���Ă���̂ŁA���s�̍��Z�w�K�w���v�͈͓̂̔��ʼn������܂��B�Ȃ��A�{��̂悤�ȁA
�͐����A�Ƃ����w�肪���Ă���̂ŁA���s�̍��Z�w�K�w���v�͈͓̂̔��ʼn������܂��B�Ȃ��A�{��̂悤�ȁA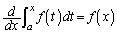 �𗘗p������ł́A��ϕ���0�ɂ���悤��x�̒l�������邱�Ƃɂ��A�B�ꂽ�������o�Ă���̂Œ��ӂ��Ă��������B�{��ł��A(3)��b�̒l�����߂�Ƃ���ōl���邱�ƂɂȂ�܂��B
�𗘗p������ł́A��ϕ���0�ɂ���悤��x�̒l�������邱�Ƃɂ��A�B�ꂽ�������o�Ă���̂Œ��ӂ��Ă��������B�{��ł��A(3)��b�̒l�����߂�Ƃ���ōl���邱�ƂɂȂ�܂��B
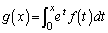 �@����@
�@����@
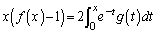 �@����A
�@����A(1) �@���ӂ�x�Ŕ�������ƁA
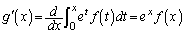 �@����B
�@����B�A���ӂ�x�Ŕ�������ƁA
���̌`�̂܂ܔ�������ƁA�E�ӂ̔�����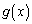 ���c���č��邱�ƂɂȂ�܂��B(1)�́A�@�C�A���
���c���č��邱�ƂɂȂ�܂��B(1)�́A�@�C�A���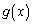 ���������邱�Ƃ��ړI�Ȃ̂ŁA�B���l�����āA�C���ӂ�
���������邱�Ƃ��ړI�Ȃ̂ŁA�B���l�����āA�C���ӂ�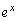 �������A
�������A 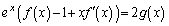 �@����D
�@����D���̗��ӂ�x�Ŕ�������ƁA
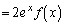 �@(�� �B)
�@(�� �B)���ӂ�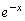 �������āA
�������āA �� 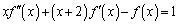
(2) 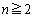 �Ƃ���
�Ƃ���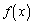 ��n���̐����Ƃ��A
��n���̐����Ƃ��A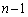 ���ȉ��̐���
���ȉ��̐���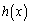 �ƒ萔a��p���āA
�ƒ萔a��p���āA �Ƃ������Ɖ��肵�܂��B
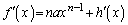 �C
�C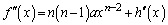
��(1)�̓����ɑ������ƁA
�������āA
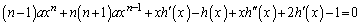 �@����E
�@����E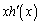 �C
�C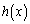 ��
��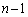 ���ȉ��A
���ȉ��A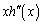 �C
�C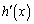 ��
��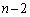 ���ȉ��̐����Ȃ̂ŁA�E��
���ȉ��̐����Ȃ̂ŁA�E��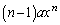 �ȊO�̍���
�ȊO�̍���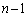 ���ȉ��̐����ɂȂ�܂��B�E���C�ӂ̎���x�ɂ��Đ������邽�߂ɂ́A
���ȉ��̐����ɂȂ�܂��B�E���C�ӂ̎���x�ɂ��Đ������邽�߂ɂ́A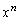 �̌W����0�łȂ���Ȃ�܂���(�P�������Q��)�B�ł����A
�̌W����0�łȂ���Ȃ�܂���(�P�������Q��)�B�ł����A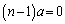 �ł́A
�ł́A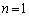 �ɂ���A
�ɂ���A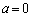 �ɂ���A
�ɂ���A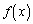 ��n��(
��n��(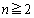 )�̐����ł��邱�Ƃɖ������܂��B
)�̐����ł��邱�Ƃɖ������܂��B
����āA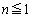 �ł���A
�ł���A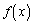 �͒萔�܂���1�����ł��B
�͒萔�܂���1�����ł��B
������(1)�̓����ɑ������ƁA
�� 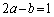 �@����F
�@����F
�@��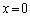 ��������ƁA
��������ƁA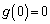 �@(
�@(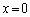 ��������̂́A�@�̒�ϕ��̒l��0�ɂ��邽��)�D��
��������̂́A�@�̒�ϕ��̒l��0�ɂ��邽��)�D��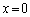 ��������ƁA
��������ƁA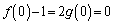
�� 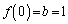 �F���A
�F���A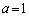
�� 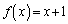 ......[��]�D���A
......[��]�D���A 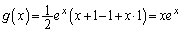 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B