���㎕�吔�w'09�N[1]
���W���ʂ܂��͍��W��Ԃɂ����āA���W���������ׂĐ����ł���_���i�q�_�Ƃ����B�ȉ��̊e�₢�ɓ�����B
(1) 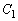 �����W���ʏ�̔��a
�����W���ʏ�̔��a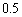 �̉~�Ƃ���B
�̉~�Ƃ���B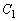 �������Ɋi�q�_���܂܂Ȃ��Ƃ��A
�������Ɋi�q�_���܂܂Ȃ��Ƃ��A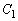 �̒��S
�̒��S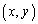 �����݂�����̈��
�����݂�����̈��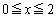 �C
�C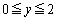 �͈̔͂Ő}������B
�͈̔͂Ő}������B (2) 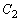 �����W���ʏ�̔��a
�����W���ʏ�̔��a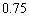 �̉~�Ƃ���B
�̉~�Ƃ���B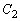 �͒��S���ǂ̂悤�Ȉʒu�Ɉړ������Ă��K�������Ɋi�q�_���܂ނ��Ƃ��ؖ�����B
�͒��S���ǂ̂悤�Ȉʒu�Ɉړ������Ă��K�������Ɋi�q�_���܂ނ��Ƃ��ؖ�����B (3) S�����W��ԓ��̔��ar�̋��Ƃ���BS�͔��a��ω��������ɒ��S���ǂ̂悤�Ȉʒu�Ɉړ������Ă��A�K�������Ɋi�q�_���܂ނ��̂Ƃ���B���̂Ƃ�r�̂Ƃ肤��l�͈̔͂����߂�B������S�̓����Ƃ́AS�̒��S����̋�����r��菬�����_�S�̂���Ȃ�W���̂��Ƃł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶�̌����Ă��邱�Ƃ͒����I�ɔ[���ł��܂����A��������_�����悤�Ƃ���Ɠ���A�Ƃ������ł��B
(1) ���a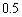 �C���S
�C���S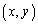 �̉~
�̉~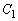 �������Ɋi�q�_
�������Ɋi�q�_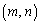 (m�Cn������)���܂ނƂ��A
(m�Cn������)���܂ނƂ��A 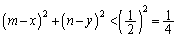 �@����@�@(�̈����Q��)
�@����@�@(�̈����Q��)�@����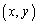 ���W���́A
���W���́A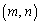 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a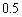 �̉~�̓����̓_�̏W���ƌ��邱�Ƃ��ł��܂��B���̏W����
�̉~�̓����̓_�̏W���ƌ��邱�Ƃ��ł��܂��B���̏W����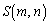 �Ƃ��܂��B
�Ƃ��܂��B 
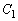 �������Ɋi�q�_���܂܂Ȃ�(
�������Ɋi�q�_���܂܂Ȃ�(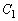 ��������
��������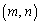 ���܂܂Ȃ��A�A���Am�Cn�͂��ׂĂ̐���)
���܂܂Ȃ��A�A���Am�Cn�͂��ׂĂ̐���) �� ������ ���� 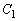 ��������
��������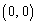 ���܂܂Ȃ� ����
���܂܂Ȃ� ���� 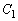 ��������
��������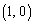 ���܂܂Ȃ� ����
���܂܂Ȃ� ���� 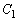 ��������
��������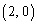 ���܂܂Ȃ� ����
���܂܂Ȃ� ���� 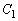 ��������
��������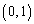 ���܂܂Ȃ� ����
���܂܂Ȃ� ���� 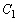 ��������
��������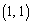 ���܂܂Ȃ� ����
���܂܂Ȃ� ���� 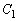 ��������
��������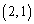 ���܂܂Ȃ� ����
���܂܂Ȃ� ���� 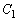 ��������
��������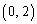 ���܂܂Ȃ� ����
���܂܂Ȃ� ���� 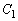 ��������
��������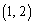 ���܂܂Ȃ� ����
���܂܂Ȃ� ���� 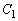 ��������
��������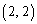 ���܂܂Ȃ� ���� ������
���܂܂Ȃ� ���� ������ �� 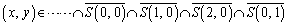
�� 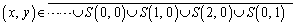
�� 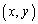 �́u������ �܂���
�́u������ �܂��� 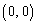 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a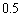 �̉~�̓��� �܂���
�̉~�̓��� �܂��� 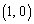 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a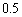 �̉~�̓��� �܂���
�̉~�̓��� �܂��� 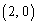 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a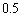 �̉~�̓��� �܂���
�̉~�̓��� �܂��� 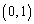 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a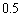 �̉~�̓��� �܂���
�̉~�̓��� �܂��� 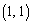 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a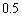 �̉~�̓��� �܂���
�̉~�̓��� �܂��� 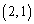 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a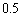 �̉~�̓��� �܂���
�̉~�̓��� �܂��� 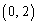 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a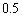 �̉~�̓��� �܂���
�̉~�̓��� �܂��� 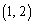 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a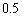 �̉~�̓��� �܂���
�̉~�̓��� �܂��� 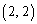 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a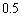 �̉~�̓��� �܂��� �������v�ł͂Ȃ�
�̉~�̓��� �܂��� �������v�ł͂Ȃ� �� 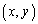 �́u�i�q�_�𒆐S�Ƃ��邷�ׂẲ~�v�̎��ォ��O��
�́u�i�q�_�𒆐S�Ƃ��邷�ׂẲ~�v�̎��ォ��O�� ����āA�͈͂Ő}������ƁA�E�}���ΐF���F�����B
(2) ���a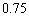 �C���S
�C���S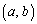 �̉~
�̉~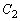 �̓����̓_�́A
�̓����̓_�́A 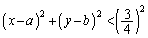 �@����A
�@����A�����܂��B(1)�̐}�����ʂ����Ă���ƁA�ׂ荇��4�̊i�q�_��4���_�Ƃ���1��1�̐����`�̗̈�ł́A4�̊i�q�_�𒆐S�Ƃ���4�~������o���Ă��邱�Ƃ��킩��܂��B�]���āA���W���ʂ��A�ׂ荇��4�̊i�q�_�_�Ƃ���1��1�̐����`�ɕ����A���̐����`�̈�����A�ǂ̊i�q�_���ł��߂����ɂ���Ă����4�ɕ����čl����悢���ƂɂȂ�܂��B���̂��߂ɁA�K�E�X�̋L�������čl���܂��B
�A��a�Cb�ɑ��āA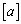 �C
�C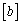 ��a�Cb���Ȃ��ő�̐����Ƃ��āA
��a�Cb���Ȃ��ő�̐����Ƃ��āA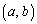 ���܂�1��1�̐����`�̉��X�~�̓_�̍��W�́A
���܂�1��1�̐����`�̉��X�~�̓_�̍��W�́A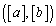 �ƕ\���܂��B�����ŁAa�Cb��C�ӂ̎����Ƃ��A�~
�ƕ\���܂��B�����ŁAa�Cb��C�ӂ̎����Ƃ��A�~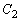 �̒��S�̍��W
�̒��S�̍��W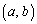 �ɑ��āA���̐����`���ȉ���4�ɕ����čl���邱�Ƃɂ��܂��B
�ɑ��āA���̐����`���ȉ���4�ɕ����čl���邱�Ƃɂ��܂��B (i) 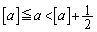 �C
�C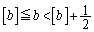 �̂Ƃ��A
�̂Ƃ��A �A�ɂ����āA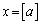 �C
�C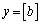 �Ƃ���ƁA
�Ƃ���ƁA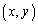 �͊i�q�_�ł��B���̂Ƃ��A
�͊i�q�_�ł��B���̂Ƃ��A 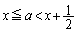 �C
�C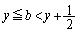
�Ȃ̂ŁA
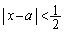 �C
�C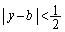
���A
����́A�i�q�_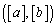 ���A�������Ƃ��Ӗ����܂��B�܂�A�~
���A�������Ƃ��Ӗ����܂��B�܂�A�~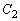 �͓����Ɋi�q�_���܂݂܂��B
�͓����Ɋi�q�_���܂݂܂��B (ii) 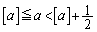 �C
�C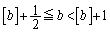 �̂Ƃ��A
�̂Ƃ��A �A�ɂ����āA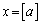 �C
�C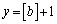 �Ƃ���ƁA
�Ƃ���ƁA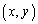 �͊i�q�_�ł��B���̂Ƃ��A
�͊i�q�_�ł��B���̂Ƃ��A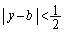
���A ����āA�~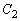 �͓����Ɋi�q�_���܂݂܂��B
�͓����Ɋi�q�_���܂݂܂��B (iii) 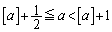 �C
�C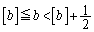 �̂Ƃ��A
�̂Ƃ��A �A�ɂ����āA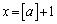 �C
�C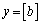 �Ƃ���ƁA
�Ƃ���ƁA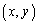 �͊i�q�_�ł��B���̂Ƃ��A
�͊i�q�_�ł��B���̂Ƃ��A ����āA�~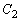 �͓����Ɋi�q�_���܂݂܂��B
�͓����Ɋi�q�_���܂݂܂��B (iv) 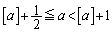 �C
�C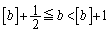 �̂Ƃ��A
�̂Ƃ��A �A�ɂ����āA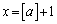 �C
�C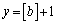 �Ƃ���ƁA
�Ƃ���ƁA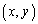 �͊i�q�_�ł��B���̂Ƃ��A
�͊i�q�_�ł��B���̂Ƃ��A ����āA�~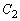 �͓����Ɋi�q�_���܂݂܂��B
�͓����Ɋi�q�_���܂݂܂��B �~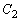 �̒��S���ǂ̂悤�Ȉʒu�Ɉړ������Ă��A��L��4�ʂ�̂����ꂩ�ł����āA�K�������Ɋi�q�_���܂݂܂��B
�̒��S���ǂ̂悤�Ȉʒu�Ɉړ������Ă��A��L��4�ʂ�̂����ꂩ�ł����āA�K�������Ɋi�q�_���܂݂܂��B
(3) ��S�̒��S��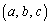 �Ƃ��āAS�����̓_�́A
�Ƃ��āAS�����̓_�́A 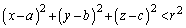 �@����B
�@����B�����܂��B(2)�Ɠ��l�ɁA
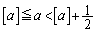 �̂Ƃ�
�̂Ƃ�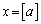
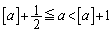 �̂Ƃ�
�̂Ƃ�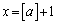
������A
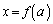 �@����C
�@����C�ƕ\�����Ƃɂ��܂��B
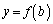 �C
�C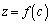
�Ƃ���A�_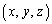 �͊i�q�_�ł��B���̂Ƃ��A
�͊i�q�_�ł��B���̂Ƃ��A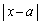 �C
�C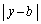 �C
�C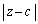 �́A�������0����
�́A�������0����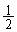 �܂ł̂��ׂĂ̎����l���Ƃ蓾�܂��B�]���āA
�܂ł̂��ׂĂ̎����l���Ƃ蓾�܂��B�]���āA ����āAa�Cb�Cc���C�ӂ̎����l���Ƃ�Ƃ��A�B���������邽�߂ɂ́A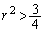 �C�����A
�C�����A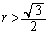 �ł��邱�Ƃ��K�v�\���ł�(�\�����u
�ł��邱�Ƃ��K�v�\���ł�(�\�����u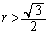 �ł����S�������Ɋi�q�_���܂ށv�͖��炩)�B
�ł����S�������Ɋi�q�_���܂ށv�͖��炩)�B
�� 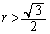 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B