������H���w'09�N���[2]
���̖₢�ɓ�����B
(1) 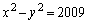 ���݂������̐���x�Cy�̑g�����ׂċ��߂�B
���݂������̐���x�Cy�̑g�����ׂċ��߂�B (2)  ���݂������̐���x�Cy�̑g�����ׂċ��߂�B
���݂������̐���x�Cy�̑g�����ׂċ��߂�B (3) 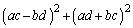 ��������������B
��������������B (4) n�𐳂̐����Ƃ���B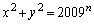 ���݂������̐���x�Cy�����݂��邱�Ƃ������B
���݂������̐���x�Cy�����݂��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(4)�ł́A(3)�̗��p�̎d���ŏ��X�Y�ނ����m��܂���B
2009��7�̔{���ł��B�Ȃ��A�����A�����������Q�Ƃ��Ă��������B
(1) 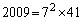 �ł��B
�ł��B ���A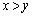 �ł����āA�ȉ���3�̏ꍇ�Ɍ����܂��B
�ł����āA�ȉ���3�̏ꍇ�Ɍ����܂��B (i) 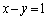 �C
�C
�A�����ĉ����ƁA
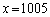 �C
�C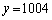
(ii)  �C
�C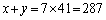
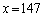 �C
�C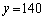
(iii)  �C
�C
 �C
�C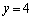
�� 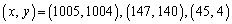 ......[��]
......[��]
(2)  ���A
���A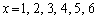 �Ɍ����܂��B
�Ɍ����܂��B ���̂����Ay�����̐����ɂȂ�̂́A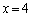 �C
�C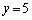 �̏ꍇ�ƁA
�̏ꍇ�ƁA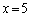 �C
�C �̏ꍇ�݂̂ł��B
�̏ꍇ�݂̂ł��B  ......[��]
......[��]
(3) 
(4) (2)���A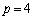 �C
�C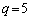 �Ƃ��āA
�Ƃ��āA 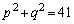 �@����@
�@����@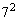 �������āA
�������āA �@����A
�@����A�ƂȂ�̂ŁA�@�� �������āA
�������āA �Ƃł��Ȃ����A�ƁA�l���Ă݂܂��B
����́A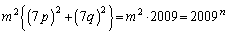
�ƂȂ�̂ŁA �ł���K�v������܂����A41���l�b�N�ƂȂ��āAm�𐮐��ɂł�����������܂���B�����ŁA(3)���ǂ��ɂ�����̂��낤�A�Ƃ������ƂɂȂ�܂��B
�܂��A�A�ɂ��ƁA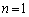 �̏ꍇ�ɁA
�̏ꍇ�ɁA �C
�C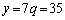 �Ƃ���A
�Ƃ���A �ɂȂ�킯�ŁA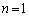 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A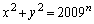 ���݂���x�Cy�����݂��܂��B
���݂���x�Cy�����݂��܂��B
 �̏ꍇ�ɂ́A�A��2�悵�āA
�̏ꍇ�ɂ́A�A��2�悵�āA 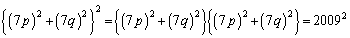 �@����B
�@����B�ƂȂ�܂����A�����ŁA(3)���g���āA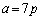 �C
�C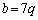 �C
�C �C
�C �Ƃ���ƁA
�Ƃ���ƁA �Ƃł���̂ŁA
�Ƃ���A
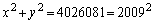 �@����C
�@����C
�Ƃł��邱�ƂɂȂ�܂��B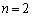 �̏ꍇ�ɂ��A
�̏ꍇ�ɂ��A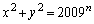 ���݂���x�Cy�����݂��܂��B
���݂���x�Cy�����݂��܂��B
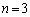 �̏ꍇ�ɂ́A�C�́A
�̏ꍇ�ɂ́A�C�́A �ɂ���ɁA�A�� �������čs�����ƂɂȂ�܂��B
�������čs�����ƂɂȂ�܂��B ���̍��ӂ��A(3)���g���āA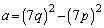 �C
�C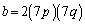 �C
�C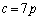 �C
�C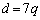 �Ƃ��ĕό`����ƁA
�Ƃ��ĕό`����ƁA �Ƃł���̂ŁA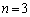 �̏ꍇ�ɂ��A
�̏ꍇ�ɂ��A ���݂���x�Cy�����݂��܂��B
���݂���x�Cy�����݂��܂��B
���Ƃ́A���̗�����A�A���Q������p���āA���w�I�A�[�@�̘g�g�݂ɓ����悢�킯�ł��B�ȉ��̂悤�ȓ��Ăɂ܂Ƃ߂���ł��傤�Bn�𐳂̐����Ƃ���Ƃ��A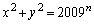 ���݂������̐���
���݂������̐��� �C
�C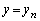 �����݂��邱�Ƃ𐔊w�I�A�[�@�ɂ�莦���B
�����݂��邱�Ƃ𐔊w�I�A�[�@�ɂ�莦���B (�T) 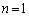 �̂Ƃ��A
�̂Ƃ��A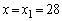 �C
�C �Ƃ���A
�Ƃ���A ���A���藧�B
���A���藧�B (�U) 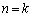 �̂Ƃ��A
�̂Ƃ��A ���݂������̐���
���݂������̐���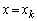 �C
�C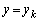 �����݂���Ɖ��肷��B
�����݂���Ɖ��肷��B �܂�A
���̗��ӂɁA ��������ƁA
��������ƁA ���A
�Ƃ���A
����āA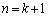 �̂Ƃ����A
�̂Ƃ����A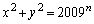 ���݂������̐���
���݂������̐��� �C
�C �����݂���B
�����݂���B (�T)�C(�U)���An�𐳂̐����Ƃ���Ƃ��A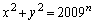 ���݂������̐���
���݂������̐���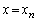 �C
�C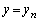 �����݂���B
�����݂���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B