������o�ϐ��w'09�N[4]
t��0�łȂ������Ƃ��Axy���ʏ�̉~ ��C�Ƃ���B���̖₢�ɓ�����B
��C�Ƃ���B���̖₢�ɓ�����B
(1) �����Ȃ�t�Ɋւ��Ă�C���ڂ���悤�Ȓ�~������1���݂��邱�Ƃ������B
(2) (1)�̒�~��C�̐ړ_�̍��W�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2�~�̈ʒu�W�̖��ł��B2�~���O�ڂ���Ƃ��A2�~�̔��a�̘a�͒��S�ԋ����Ɉ�v���A�Е��̉~�������̉~�ɓ��ڂ���Ƃ��A2�~�̔��a�̍��͒��S�ԋ����Ɉ�v���܂��B
(1) C�F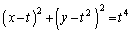 �@(
�@(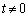 )�@����@
)�@����@ (i) C�����S �C���ar�̉~�ɊO�ڂ���Ƃ��A���S�ԋ����F
�C���ar�̉~�ɊO�ڂ���Ƃ��A���S�ԋ����F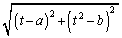 ���A2�~�̔��a�̘a
���A2�~�̔��a�̘a �ɓ������A
�ɓ������A ���ӂ�2�悷��ƁA
t�ɂ��Đ�������ƁA
 �@����A
�@����A�����ŁA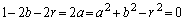 �̂Ƃ�(�P�������Q��)�A
�̂Ƃ�(�P�������Q��)�A
�܂�A �̂Ƃ��A�A�͂����Ȃ�t�ɑ��Ă��������܂��B
����́A�~C���A�����Ȃ�t�ɑ��Ă��A��~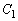 �F
�F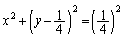 �@����B�@�ɊO�ڂ��邱�Ƃ��Ӗ����܂��B
�@����B�@�ɊO�ڂ��邱�Ƃ��Ӗ����܂��B (ii) C�̔��a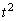 �͂�����ł��傫���Ȃ�̂ŁA�u�����Ȃ�t�Ɋւ��Ă��~C�����ڂ���v�~�͂��蓾�܂���B
�͂�����ł��傫���Ȃ�̂ŁA�u�����Ȃ�t�Ɋւ��Ă��~C�����ڂ���v�~�͂��蓾�܂���B ���S �C���ar�̉~���~C�ɓ��ڂ���Ƃ��A2�~�̔��a�̍������S�ԋ����ɓ������A
�C���ar�̉~���~C�ɓ��ڂ���Ƃ��A2�~�̔��a�̍������S�ԋ����ɓ������A t�ɂ��Đ�������ƁA
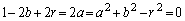 �Ƃ���ƁA
�Ƃ���ƁA �Ȃ̂ŁA�������r�͂���܂���B
�Ȃ̂ŁA�������r�͂���܂���B
�܂�A�u�����Ȃ�t�Ɋւ��Ă��~C�ɓ��ڂ���v��~�͂���܂���B(i)�C(ii)���A�����Ȃ�t�Ɋւ��Ă�C���ڂ���悤�Ȓ�~������1���݂��܂��B
(2) (1)�̒�~��C�̐ړ_�́A���~�̒��S�����Ԓ�����ɂ���܂��B
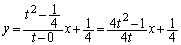 �@����C
�@����C���̒����Ɖ~ �̌�_�́A
�̌�_�́A �̂Ƃ��A�B�C�C��A�����āA
�̂Ƃ��A�B�C�C��A�����āA �� 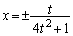 �ړ_�́A���~�̒��S�̊Ԃɂ���̂ŁA
�ړ_�́A���~�̒��S�̊Ԃɂ���̂ŁA �C�܂��́A
�C�܂��́A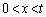 ���A
���A ���̂Ƃ��A�C���A
���߂�ړ_�̍��W�́A ......[��]���D�ړ_�́A
......[��]���D�ړ_�́A �C
�C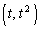 �a�̔�
�a�̔� �F
�F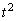 ����������_�ł��B
����������_�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B