��t�吔�w'10�N[11]
 �͎����S�̂Œ�`���ꂽ���Ƃ���B����a�Ɋւ������(P)���l����B
�͎����S�̂Œ�`���ꂽ���Ƃ���B����a�Ɋւ������(P)���l����B
(P) ���̎���r���\���������I�ׂA ���݂������ׂĂ̎���x�ɑ���
���݂������ׂĂ̎���x�ɑ���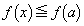 �����藧�B
�����藧�B ���̂Ƃ��A�ȉ��̖₢�ɓ�����B
(1) ����a������(P)���݂����A���A ��
�� �Ŕ����\�Ȃ�A
�Ŕ����\�Ȃ�A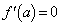 �ł��邱�Ƃ��ؖ�����B
�ł��邱�Ƃ��ؖ�����B (2) ��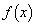 ��
�� �Œ�`����Ă���Ƃ��A����(P)���݂����悤�Ȏ���a�S�̂̏W�������肹��B
(3) ��ʂɁA�����S�̂Œ�`���ꂽ��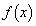 �ɑ��A���̖���͐��������B��������Ώؖ����A�������Ȃ���Δ����������B
�ɑ��A���̖���͐��������B��������Ώؖ����A�������Ȃ���Δ����������B (����) ���ׂĂ̎���a������(P)���݂����Ȃ�A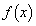 �͒萔���ł���B
�͒萔���ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�{�i�I�Ȑ��w�̍��肪�Y�����ł����A������Ȃ����Ȃ̂ŁA�ǂ�����ē��Ă��������Y�ނ����m��܂���B�Ȃ��A�ؖ��̋Z�I���Q�Ƃ��Ă��������B
�ȉ��ŁA
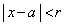 ��
��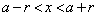
(1)  �ɂ����āA
�ɂ����āA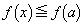 �ł��B
�ł��B �܂��A ��
��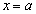 �Ŕ����\�Ȃ̂ŁA�Ɍ��l
�Ŕ����\�Ȃ̂ŁA�Ɍ��l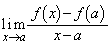 �����݂��āA
�����݂��āA �ł��B
�����ŁA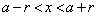 ���A
���A ��
�� ��2�̕����ɕ����čl���܂��B
��2�̕����ɕ����čl���܂��B �� �@����B
�@����B �@�C�A�C�B���A
 �@(�ؖ��I)
�@(�ؖ��I)
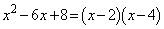 ���A
���A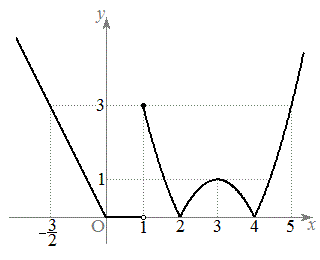 �������A
�������A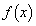 �̃O���t�͉E�}�̂悤�ɂȂ�܂��B������A�ȉ��̂悤��a�͈̔͂��čl���܂��B
�̃O���t�͉E�}�̂悤�ɂȂ�܂��B������A�ȉ��̂悤��a�͈̔͂��čl���܂��B(i)  �̂Ƃ��A
�̂Ƃ��A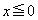 �ɂ�����
�ɂ����� �͌������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r�ɑ��Ă��A
�͌������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r�ɑ��Ă��A ����x�̂����A�Ⴆ��
����x�̂����A�Ⴆ�� �ɂ��āA
�ɂ��āA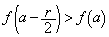 �ƂȂ�A����(P)�͐������܂���B
�ƂȂ�A����(P)�͐������܂���B (a) 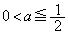 �̂Ƃ��A
�̂Ƃ��A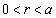 �ƂȂ�悤��r���Ƃ�A
�ƂȂ�悤��r���Ƃ�A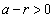 �C
�C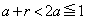 ���A
���A  �������ׂĂ̎���x�ɑ��āA
�������ׂĂ̎���x�ɑ��āA �ŁA����(P)���������܂��B
�ŁA����(P)���������܂��B(b) 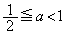 �̂Ƃ��A
�̂Ƃ��A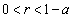 �ƂȂ�悤��r���Ƃ�A
�ƂȂ�悤��r���Ƃ�A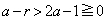 �C
�C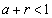 ���A
���A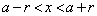 �������ׂĂ̎���x�ɑ��āA
�������ׂĂ̎���x�ɑ��āA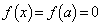 �ŁA����(P)���������܂��B
�ŁA����(P)���������܂��B (iii) 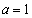 �̂Ƃ��A
�̂Ƃ��A �Ȃ̂ŁA
�Ȃ̂ŁA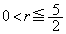 ����r���Ƃ�A
����r���Ƃ�A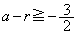 �C
�C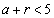 ���A
���A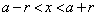 �������ׂĂ̎���x�ɑ��āA
�������ׂĂ̎���x�ɑ��āA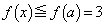 (�E�}���Q��)�ŁA����(P)���������܂��B
(�E�}���Q��)�ŁA����(P)���������܂��B (iv)  �̂Ƃ��A
�̂Ƃ��A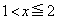 �ɂ�����
�ɂ�����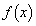 �͌������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r (
�͌������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r (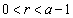 )�ɑ��Ă��A
)�ɑ��Ă��A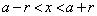 ����x�̂����A�Ⴆ��
����x�̂����A�Ⴆ��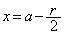 �ɂ��āA
�ɂ��āA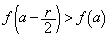 �ƂȂ�̂ŁA����(P)�͐������܂���B
�ƂȂ�̂ŁA����(P)�͐������܂���B (v) 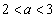 �̂Ƃ��A
�̂Ƃ��A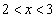 �ɂ�����
�ɂ�����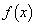 �͑������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r (
�͑������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r ( )�ɑ��Ă��A
)�ɑ��Ă��A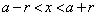 ����x�̂����A�Ⴆ��
����x�̂����A�Ⴆ��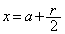 �ɂ��āA
�ɂ��āA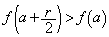 �ƂȂ�̂ŁA����(P)�͐������܂���B
�ƂȂ�̂ŁA����(P)�͐������܂���B (vi) 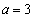 �̂Ƃ��A
�̂Ƃ��A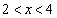 �ɂ�����
�ɂ�����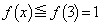 �Ȃ̂ŁA
�Ȃ̂ŁA �ƂȂ�悤��r���Ƃ�A
�ƂȂ�悤��r���Ƃ�A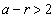 �C
�C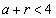 ���A
���A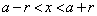 �������ׂĂ̎���x�ɑ��āA
�������ׂĂ̎���x�ɑ��āA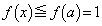 �ŁA����(P)���������܂��B
�ŁA����(P)���������܂��B (vii) 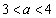 �̂Ƃ��A
�̂Ƃ��A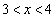 �ɂ�����
�ɂ����� �͌������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r (
�͌������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r (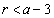 )�ɑ��Ă��A
)�ɑ��Ă��A ����x�̂����A�Ⴆ��
����x�̂����A�Ⴆ��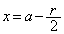 �ɂ��āA
�ɂ��āA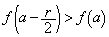 �ƂȂ�̂ŁA����(P)�͐������܂���B
�ƂȂ�̂ŁA����(P)�͐������܂���B (viii)  �̂Ƃ��A
�̂Ƃ��A �ɂ�����
�ɂ�����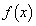 �͑������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r�ɑ��Ă��A
�͑������Ȃ̂ŁA�ǂ�ȏ����Ȑ���r�ɑ��Ă��A ����x�̂����A�Ⴆ��
����x�̂����A�Ⴆ��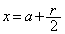 �ɂ��āA
�ɂ��āA �ƂȂ�̂ŁA����(P)�͐������܂���B
�ƂȂ�̂ŁA����(P)�͐������܂���B �ȏ���A����(P)�����悤�Ȏ���a�S�̂̏W���́A
 ......[��]
......[��]
(3) �萔���ł���Ώ���(P)�������ƁA�܂��A�A���������ł���͈́A�A���������ł���͈͂������ł͏���(P)����������Ȃ����Ƃ͖��炩�ł��B
(2)��(iii)�̏ꍇ�ł�����(P)���������邱�Ƃ��l����ƁA���ɕs�A���_�������āA���̕s�A���_���܂ޓK���Ȕ͈͓��ŁA���̕s�A���_�ɂ����čő�ƂȂ��Ă��āA�s�A���_�ȊO�ł͒萔�l���Ƃ���ł���A����(P)���������܂��B
�]���āAx�������l�̂Ƃ�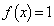 �Cx�������l�łȂ��Ƃ�
�Cx�������l�łȂ��Ƃ�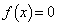 �ƂȂ�悤�Ȋ�
�ƂȂ�悤�Ȋ�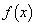 �ł́A�萔���ł͂Ȃ��̂ɁA���ׂĂ̎���a������(P)�����܂��B
�ł́A�萔���ł͂Ȃ��̂ɁA���ׂĂ̎���a������(P)�����܂��B
����͐������Ȃ��B����́Ax�������l�̂Ƃ� �Cx�������l�łȂ��Ƃ�
�Cx�������l�łȂ��Ƃ�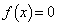 �ƂȂ�悤�Ȋ�
�ƂȂ�悤�Ȋ�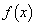 ......[��]
......[��] ���D��L�̔���ŁA���������A�ق�̂�����Ƃ�������������a�A���邢�́A�ق�̂�����Ƃ����傫������a�̂Ƃ��A����(P)�͐��藧���Ȃ��̂ł͂Ȃ����A�ƁA������l�����邩���m��܂���B
�ł����A������n�Ƃ��āA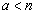 �ƂȂ�悤��a���A�ǂ�Ȃ�n�̋߂��Ƃ��Ă��Ar��
�ƂȂ�悤��a���A�ǂ�Ȃ�n�̋߂��Ƃ��Ă��Ar��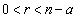 �ƂȂ�悤�ɂƂ��(
�ƂȂ�悤�ɂƂ��( �Ƃ��܂�)�A
�Ƃ��܂�)�A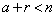 �Ȃ̂ŁA
�Ȃ̂ŁA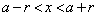 �������ׂĂ̎���x�ɑ���
�������ׂĂ̎���x�ɑ���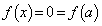 �ƂȂ����(P)���������܂��B
�ƂȂ����(P)���������܂��B
�܂��A �ƂȂ�悤��a���A�ǂ�Ȃ�n�̋߂��ɂƂ��Ă��Ar��
�ƂȂ�悤��a���A�ǂ�Ȃ�n�̋߂��ɂƂ��Ă��Ar��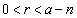 �ƂȂ�悤�ɂƂ��(
�ƂȂ�悤�ɂƂ��( �Ƃ��܂�)�A
�Ƃ��܂�)�A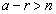 �Ȃ̂ŁA
�Ȃ̂ŁA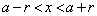 �������ׂĂ̎���x�ɑ���
�������ׂĂ̎���x�ɑ���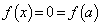 �ƂȂ����(P)���������܂��B
�ƂȂ����(P)���������܂��B
�������a�̂ǂ�Ȃɋ߂���a�ƈقȂ����b���Ƃ��Ă� �C�܂��́A
�C�܂��́A ��������c���Ƃ��A�Ƃ��������̐������A�������f�����ƌ����܂��B
��������c���Ƃ��A�Ƃ��������̐������A�������f�����ƌ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B