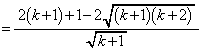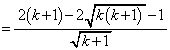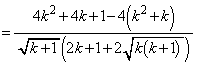�����嗝���w'10�N[7]
���R��n�ɑ��āA
�����藧���Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�K�i�^���̃O���t�ɂ��s�������ؖ����܂��B���w�I�A�[�@�ɂ���Ă��ؖ��\�ł��B
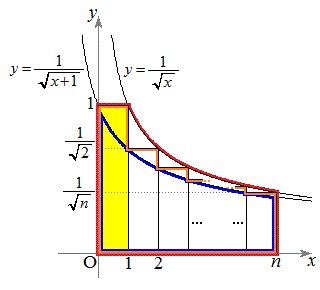 �E�}�ŁA��F���ň͂܂ꂽ�̈�̖ʐ�S�́A
�E�}�ŁA��F���ň͂܂ꂽ�̈�̖ʐ�S�́A
S�́A�E�}�ŁA�Ȑ�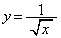 ��x���C
��x���C �C
�C �ň͂܂ꂽ�̈�ɉ��F���F�������������̈�(�ԐF���ň͂܂ꂽ�̈�)�̖ʐς���������(
�ň͂܂ꂽ�̈�ɉ��F���F�������������̈�(�ԐF���ň͂܂ꂽ�̈�)�̖ʐς���������(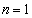 �̂Ƃ��̂݁AS�͐ԐF���ň͂܂�镔���̖ʐςɈ�v)�A�Ȑ�
�̂Ƃ��̂݁AS�͐ԐF���ň͂܂�镔���̖ʐςɈ�v)�A�Ȑ� ��x���Cy���C
��x���Cy���C �ň͂܂ꂽ�̈�(�F���ň͂܂ꂽ����)�̖ʐς����傫���A
�ň͂܂ꂽ�̈�(�F���ň͂܂ꂽ����)�̖ʐς����傫���A
�� 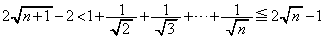
�ʉ��D���w�I�A�[�@�ɂ���Ă������܂��B
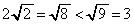 ���A
���A
����āA�^�s�����͐��藧���܂��B(�U) 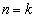 �̂Ƃ��A�^�s���������藧�Ɖ��肵�܂��B
�̂Ƃ��A�^�s���������藧�Ɖ��肵�܂��B �e�ӂ�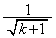 ��������ƁA
��������ƁA 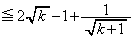 �@����@
�@����@�@�̍��ӂɂ��āA
�� 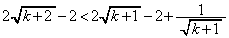 �@����A
�@����A
�@�̉E�ӂɂ��āA ��  �@����B
�@����B
�@�C�A�C�B���A ����āA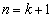 �̂Ƃ��ɂ��^�s�����͐��藧���܂��B
�̂Ƃ��ɂ��^�s�����͐��藧���܂��B (�T)�C(�U)���A���R��n�ɑ��āA�^�s���������藧���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B