��ϕ��Ɩʐ�(����2)�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A�s��ϕ��̌����A��ϕ��Ɩʐ����Q�Ƃ��Ă��������B
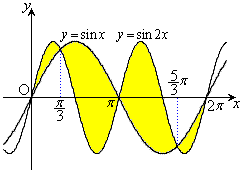 ��1�D
��1�D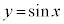 �C
�C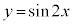 �̃O���t���A
�̃O���t���A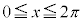 �͈̔͂ň͂ޕ����̐}�`�̖ʐς����߂�B
�͈̔͂ň͂ޕ����̐}�`�̖ʐς����߂�B
[��]�@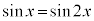 �Ƃ��āA
�Ƃ��āA
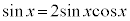
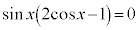
�� 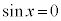 �C
�C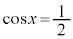
�� 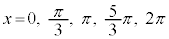
�ʐς����߂镔���́A�E�}�ʼn��F�ɓh��ꂽ�����B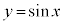 �C
�C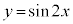 �̃O���t�́A
�̃O���t�́A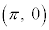 �Ɋւ��đΏ̂�����A���߂�ʐ�S�́A
�Ɋւ��đΏ̂�����A���߂�ʐ�S�́A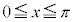 �ɂ����āA���O���t���͂ޕ����̖ʐς�2�{�ɓ������B
�ɂ����āA���O���t���͂ޕ����̖ʐς�2�{�ɓ������B
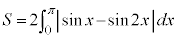
�@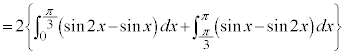
�@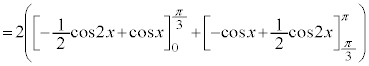
�@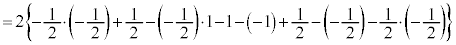
�@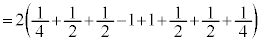
�@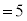 ......[��]
......[��]
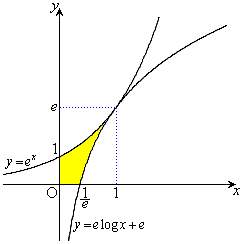 ��2�D�@2�Ȑ��A
��2�D�@2�Ȑ��A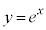 �C
�C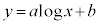 ��
��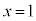 �ɂ����Đڂ���悤��a�Cb���߁A2�Ȑ���x���Cy���Ƃň͂܂�镔���̖ʐς����߂�B
�ɂ����Đڂ���悤��a�Cb���߁A2�Ȑ���x���Cy���Ƃň͂܂�镔���̖ʐς����߂�B
[��]�@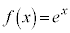 �C
�C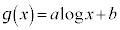 �Ƃ��āA
�Ƃ��āA
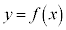 ��
��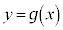 ��
��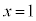 �ɂ����Đڂ���@�́@
�ɂ����Đڂ���@�́@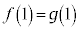 ����@ ����
����@ ���� 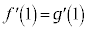 ����A
����A
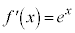 �C
�C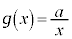
�@���A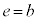
�A���A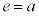
����āA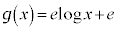
�ʐς����߂镔���͉E�}�ʼn��F���h���Ă��镔���B���߂�ʐ�S�́A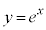 ��x���Cy���C
��x���Cy���C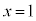 �ň͂܂�镔���̖ʐς���A
�ň͂܂�镔���̖ʐς���A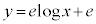 ��x���C
��x���C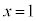 �ň͂܂�镔���̖ʐς����������̂ɂȂ�܂��B
�ň͂܂�镔���̖ʐς����������̂ɂȂ�܂��B
�܂��A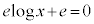 �Ƃ����ƁA
�Ƃ����ƁA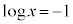 �C
�C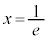 ���A
���A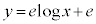 ��x����
��x����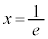 �Ō����܂��B
�Ō����܂��B
�� 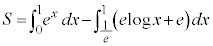
�@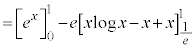
�@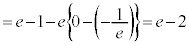 ......[��]
......[��]
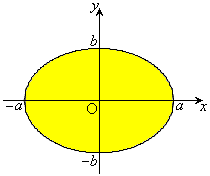 ��3�D�@�ȉ~�F
��3�D�@�ȉ~�F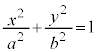 ���͂ޕ����̖ʐς����߂�B
���͂ޕ����̖ʐς����߂�B
[��]�@y�ɂ��ĉ����ƁA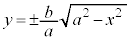
�����́{�́A�ȉ~��x������㑤�̕����A�|�́A�ȉ~��x�����牺�̕�����\���܂��B
�Ȑ��̑��ݔ͈�(��`��)�́A��������0�ȏ�Ƃ��āA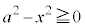 ���A
���A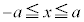
���߂�ʐ�S�́A�Ȑ��̏㑤�̕�����\�����F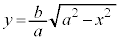 ���牺���̕��������F
���牺���̕��������F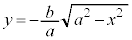 �������āA
�������āA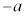 ����a�܂Őϕ�������߂��܂��B
����a�܂Őϕ�������߂��܂��B
�� 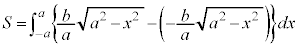
�@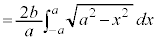
��ϕ�����y�Ƃ����ƁA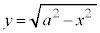
���ӂ�2�悷��ƁA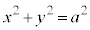 ���A���_�𒆐S�Ƃ��锼�aa�̉~�B
���A���_�𒆐S�Ƃ��锼�aa�̉~�B
����āA�ϕ��́A���aa�̉~�̖ʐς�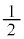 �C�����A
�C�����A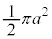 �ɓ�����(�u���ϕ�(����2)���Q��)�A
�ɓ�����(�u���ϕ�(����2)���Q��)�A
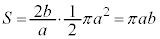 ......[��]
......[��]
���̌��ʂ́A�L�����Ă��������B
 ��4�D�@�}��ϐ��\���A
��4�D�@�}��ϐ��\���A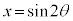 �C
�C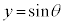 (
(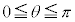 )�ɂ��^������Ȑ��̈͂ޖʐς����߂�B
)�ɂ��^������Ȑ��̈͂ޖʐς����߂�B
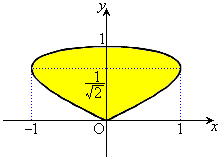
[��]�@θ ��0����π�܂œ����ԂɁAy�́A0����1�ƂȂ�0�ɖ߂�܂��Bx�́A0����1�ɂȂ�0�ɖ߂���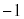 �܂ōs��0�ɖ߂�܂��B�O���t�͉E�}�̂悤�ɂȂ�܂�(���m�ɂ́A�������đ����ׂ邱�ƁB
�܂ōs��0�ɖ߂�܂��B�O���t�͉E�}�̂悤�ɂȂ�܂�(���m�ɂ́A�������đ����ׂ邱�ƁB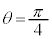 �̂Ƃ��A
�̂Ƃ��A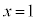 �C
�C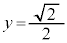 �C
�C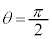 �̂Ƃ��A
�̂Ƃ��A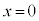 �C
�C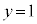 �C
�C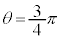 �̂Ƃ��A
�̂Ƃ��A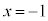 �C
�C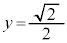 )�B
)�B
���߂�ʐ�S�́Ax��y�ɂ���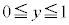 �͈̔͂Őϕ���������(
�͈̔͂Őϕ���������(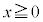 �̕����̖ʐ�)��2�{�ł��B�܂�A
�̕����̖ʐ�)��2�{�ł��B�܂�A
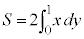
x��θ �̊��ŗ^�����Ă���̂ŁAy�ł͐ϕ����ł��܂���B�����ŁAx��θ �ŕ\���Ă����āA�u���ϕ��ɂ��Ay�̐ϕ���θ �̐ϕ��ɒ����܂��B
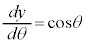 ���A
���A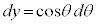 �Cy�F
�Cy�F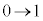 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F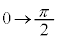
�� 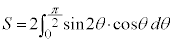
�@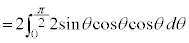
�@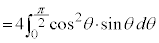
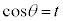 �Ƃ����ƁA
�Ƃ����ƁA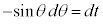 �Cθ�F
�Cθ�F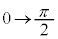 �̂Ƃ��At�F
�̂Ƃ��At�F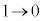
�� 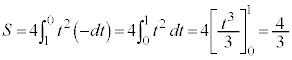 ......[��]
......[��]
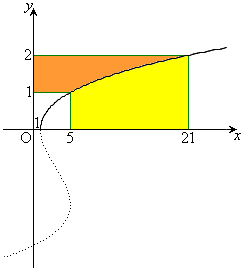 ��5�D�@�Ȑ��F
��5�D�@�Ȑ��F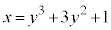 (
(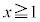 �C
�C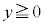 )�Cx���C����
)�Cx���C����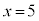 �C����
�C����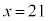 �ň͂܂�镔���̖ʐς����߂�B
�ň͂܂�镔���̖ʐς����߂�B
[��]�@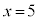 �̂Ƃ��A
�̂Ƃ��A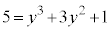
�� 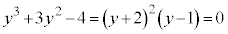
 ���A
���A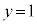
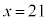 �̂Ƃ��A
�̂Ƃ��A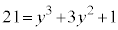
�� 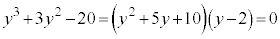
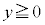 ���A
���A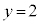
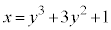 ��y�Ŕ�������ƁA
��y�Ŕ�������ƁA
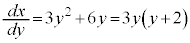
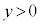 �ɂ����āA
�ɂ����āA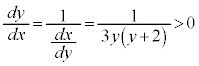 �@(�t���̔����@���Q��)
�@(�t���̔����@���Q��)
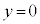 �̂Ƃ��A
�̂Ƃ��A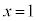
�]���āA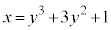 �́A
�́A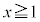 �ɂ����ĒP�������ł���A���߂�ʐ�S�́Ay��x�ŁA
�ɂ����ĒP�������ł���A���߂�ʐ�S�́Ay��x�ŁA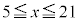 �͈̔͂Őϕ��������̂ɂȂ�܂��B
�͈̔͂Őϕ��������̂ɂȂ�܂��B
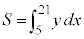
�Ƃ��낪�A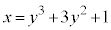 �ɂ��āAy��x�ŕ\�����Ƃ��ł��Ȃ��̂ł��B����ł́A�ϕ����v�Z�ł��܂���B
�ɂ��āAy��x�ŕ\�����Ƃ��ł��Ȃ��̂ł��B����ł́A�ϕ����v�Z�ł��܂���B
�E�}�ɂ����āA�ʐς����߂镔���͉��F�œh��ꂽ�����ł����A����́A���_O�C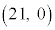 �C
�C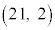 �C
�C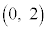 ��4���_�Ƃ��钷���`����A���_O�C
��4���_�Ƃ��钷���`����A���_O�C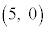 �C
�C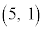 �C
�C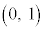 ��4���_�Ƃ��钷���`����菜���A����ɁA�Ȑ��F
��4���_�Ƃ��钷���`����菜���A����ɁA�Ȑ��F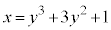 ��y���C����
��y���C����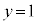 �C����
�C����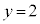 �ň͂܂��}�`A (�E�}�ɂ����Ğ�F�œh��ꂽ����)����菜�������̂ɂȂ�܂��B
�ň͂܂��}�`A (�E�}�ɂ����Ğ�F�œh��ꂽ����)����菜�������̂ɂȂ�܂��B
�}�`A�̖ʐςȂ�Ax��y�Őϕ����邱�ƂɂȂ�̂Ōv�Z�ł��܂��B�}�`A�̖ʐ�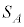 �́A
�́A
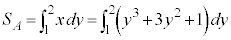
�@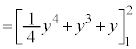
�@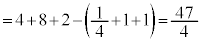
����āA���߂�ʐ�S�́A
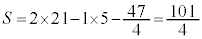 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 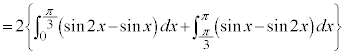
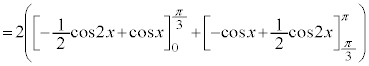
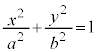 ���͂ޕ����̖ʐς����߂�B
���͂ޕ����̖ʐς����߂�B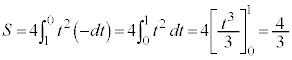 ......[��]
......[��]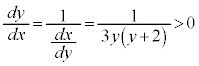 �@(�t���̔����@���Q��)
�@(�t���̔����@���Q��)