北大数学'10年前期[4]
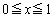に対して
と定める。ただし、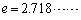
は自然対数の底である。
(1) 不定積分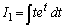
，
を求めよ。 (2)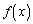 
をxの指数関数と多項式を用いて表せ。 (3) 
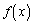は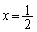
で極大となることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 単なる微積の計算問題だろうと思って安易に取り組むと、(3)で予想外の落とし穴が待っています。
(
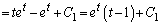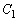：積分定数) ......[答]
(
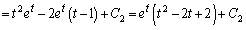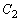：積分定数) ......[答]
(2) 
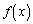の定積分は、定積分の中にある絶対値記号の内側の正負によって、積分区間を、
，
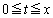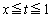の2つにわけます。
(3) 
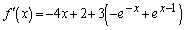
方程式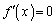
は解くことができません。
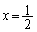を代入してみると、 これで増減表を書けば、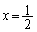
において極値をとる、と、言えそうですが、
，
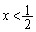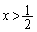において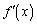
がどんな変化をするのか、
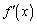の形を見ているだけではわかりません。
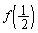が極大値ということもあり得ます。
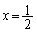において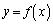
のグラフがx軸と平行な接線をもつだけで
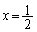の近くで
が符号を変えない、ということもあり得ます。
そこで、
を微分してみます。 注．
とすると、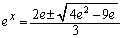
となって、2解あることがわかります。従って、xを増加させていくとき、
は、増加、減少、増加と変化します(関数の増減を参照)。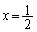 
における
の符号を調べてみます。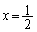
において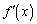
は減少していて、xを増加させていくとき、
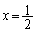の前後で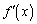
は正から負へと符号が変わります。よって、
は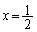
において極小となります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
より
，第2項の定積分では
より
とおくと、
，t：
のときu：
......[答]
