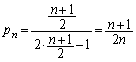兵庫県立大数学'10年[3]
数直線上の原点に点Aがある。点Aは次の規則に従って数直線上を正の向きに動いていく。
「Aが座標kの位置にあるとき数直線上の正の向きに1進む確率が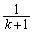 ,正の向きに2進む確率が
,正の向きに2進む確率が である。」
である。」 点Aが座標nの位置に立ち寄る確率を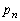 とする。このとき、次の問いに答えよ。
とする。このとき、次の問いに答えよ。
(1) 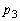 を求めよ。
を求めよ。 (2) 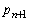 を
を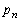 で表せ。
で表せ。 (3) 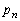 を求めよ。
を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 確率と数列の融合問題ですが、見慣れない漸化式が出てきます。予測して数学的帰納法で証明しておきましょう。
(1) Aが原点にいるとき1進む確率は、問題文中の規則で として1となるので、原点にいるときには次は必ず座標1に来ます。つまり、
として1となるので、原点にいるときには次は必ず座標1に来ます。つまり、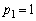
Aが座標1にいるとき、1進んで座標2に行く確率は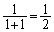 ,2進む確率は
,2進む確率は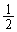 ,2進むと座標3に行き座標2には立ち寄らないので、
,2進むと座標3に行き座標2には立ち寄らないので、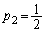 Aは確率
Aは確率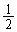 で座標2に来て、さらに1進む確率は
で座標2に来て、さらに1進む確率は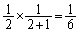 で、このとき座標3に来ます。
で、このとき座標3に来ます。
座標3に立ち寄る確率は、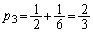 ......[答]
......[答]
(2) Aが座標nに立ち寄るとき(確率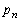 )、ここからさらに1進んで座標
)、ここからさらに1進んで座標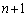 に行く確率は
に行く確率は
Aが座標nに立ち寄らないとき(確率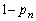 )には、必ず座標
)には、必ず座標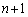 に立ち寄ります。
に立ち寄ります。
よって、座標 に立ち寄る確率
に立ち寄る確率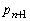 は、
は、 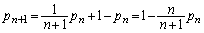 ......[答]
......[答]
これよりmを自然数として、
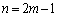 のとき、
のとき、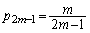
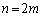 のとき、
のとき、
と予測できます。
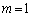 のとき、
のとき、 ,
,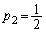 より予測は成り立ちます。
より予測は成り立ちます。
ある自然数mで予測が成り立つとして、(2)の漸化式を用いて、 よって帰納的に、予測は成り立ちます。
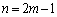 のとき
のとき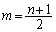 より、
より、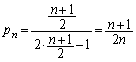
これより、nが奇数のとき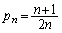 ,nが偶数のとき
,nが偶数のとき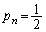 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。