広島大理系数学'10年[5]
4で割ると余りが1である自然数全体の集合をAとする。すなわち、
とする。次の問いに答えよ。
(1) xおよびyがAに属するならば、その積
もAに属することを証明せよ。 (2) 0以上の偶数mに対して、
はAに属することを証明せよ。 (3) m，nを0以上の整数とする。
が偶数ならば
はAに属し、
が奇数ならば
はAに属さないことを証明せよ。 (4) m，nを0以上の整数とする。
の正の約数のうち、Aに属する数全体の和をmとnを用いて表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 誘導なしでいきなり(4)を聞かれると厳しい問題ですが、誘導に乗って進めて行けば、解答できます。なお、集合、整数を参照してください。
(1) 
，
であれば、p，qを0以上の整数として、
，
と表すことができます。
は0以上の整数なので、となります。 (証明終)
(2) 0以上の偶数mは、kを0以上の整数として、
と表すことができます。
となりますが、
より、
です。従って、(1)より、
です。
また、(1)より、
であれば、
です。
よって、帰納的に(数学的帰納法を参照)、0以上の整数k，つまり、0以上の偶数mについて、 となります。 (証明終)
(3) 以下では、p，qを0以上の整数とします。
となりますが、(2)より、
です。
についても、
より、
で、(1)より、
，
であれば、
となり、帰納的に
となるので、(1)より、 となります。
となりますが、(i)で見たように、
なので、
(kは0以上の整数)とおくと、 は、4で割ると3余るので、
となります。
となりますが、(i)で見たように、
なので、
(kは0以上の整数)とおくと、 は、4で割ると3余るので、
となります。
となります。
以上より、
が偶数ならば
はAに属し、
が奇数ならば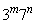
はAに属しません。 (証明終)
(4) 
の正の約数は、p，qを
，
を満たす整数として、
の形に表せます。このうち、Aに属するものは、(3)より、
が偶数となるもので、pが偶数ならqも偶数、pが奇数ならqも奇数となります。これらの和Sは、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
のとき、
は偶数です。
，
のとき、
は奇数です。
，
のとき、
は奇数です。
，
のとき、
は偶数です。
，また、
より、
なので、(1)より、
......[