�O�O�吔�w'10�N���[3]
������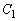 �F
�F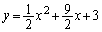 ��x���ň͂܂ꂽ�̈��
��x���ň͂܂ꂽ�̈��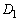 �Ƃ���B����
�Ƃ���B����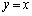 �Ɋւ���
�Ɋւ���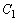 �Ɛ��Ώ̂ȕ�������
�Ɛ��Ώ̂ȕ�������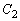 �F
�F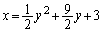 �Ƃ��A
�Ƃ��A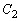 ��y���ň͂܂ꂽ�̈��
��y���ň͂܂ꂽ�̈��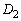 �Ƃ���B
�Ƃ���B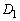 ��
��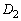 �̋��ʕ����̖ʐς����߂�B
�̋��ʕ����̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�e07�N�����C�m��A'93�N���勳��ł��o�肳�ꂽ��^�p�^�[�����ł��B
�̂��肪���������݂��݂킩��܂��B
�{��ł͌�_�̍��W�������Ȃ̂ŁA����Ȍv�Z�����Ă��ŏI�ɂ��ǂ���܂����A��_�̍��W�ɍ���������ꍇ������̂ŁA�K���ȉ��̉�@�ʼn���悤�ɂ��܂��傤�B
�܂��A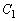 �C
�C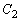 �̌�_�����߂�K�v������܂��B�@�C�A��A�����āA�@��y�̎����A��y�ɑ�������x��4���������ƂȂ��đ�ςł��B
�̌�_�����߂�K�v������܂��B�@�C�A��A�����āA�@��y�̎����A��y�ɑ�������x��4���������ƂȂ��đ�ςł��B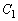 ��
��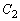 �͒���
�͒���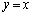 �Ɋւ��đΏ̂ȕ������Ȃ̂ŁA��_�����݂���Β���
�Ɋւ��đΏ̂ȕ������Ȃ̂ŁA��_�����݂���Β���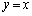 ��ɂ���_�����܂��B�ł���A�@�C�A��A������̂ł͂Ȃ��A�@��
��ɂ���_�����܂��B�ł���A�@�C�A��A������̂ł͂Ȃ��A�@��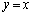 ��A�������(2���������ɂȂ�܂�)����
��A�������(2���������ɂȂ�܂�)����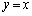 ��ɗ����_��2���߂邱�Ƃ��ł���ł��傤�B�ł����A�@�C�A��A������4���������ɂȂ�Ƃ������Ƃ́A����2��_���邩���m��܂���B�����ŁA�@�|�A������Ă݂܂��B3����������āA�c��̍��͂ǂ��
��ɗ����_��2���߂邱�Ƃ��ł���ł��傤�B�ł����A�@�C�A��A������4���������ɂȂ�Ƃ������Ƃ́A����2��_���邩���m��܂���B�����ŁA�@�|�A������Ă݂܂��B3����������āA�c��̍��͂ǂ��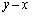 �������ɂ���(����
�������ɂ���(����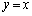 ��Ɍ�_�����݂���)���Ƃɒ��ڂ��܂��B�@�|�A���A
��Ɍ�_�����݂���)���Ƃɒ��ڂ��܂��B�@�|�A���A
�� 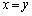 �܂���
�܂��� 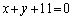
�@�ɂ����āA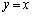 �Ƃ���ƁA
�Ƃ���ƁA
�� 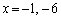
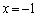 �̂Ƃ�
�̂Ƃ�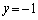 �C
�C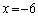 �̂Ƃ�
�̂Ƃ�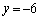 �ł��B
�ł��B
�@�ɂ����āA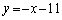 �Ƃ���ƁA
�Ƃ���ƁA
�� 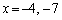
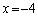 �̂Ƃ�
�̂Ƃ�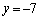 �C
�C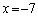 �̂Ƃ�
�̂Ƃ�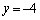 �ł��B
�ł��B
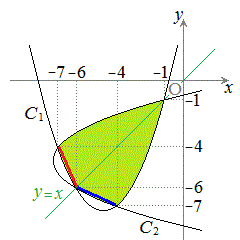
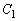 �C
�C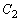 �̈ʒu�W��}������ƉE�}�̂悤�ɂȂ��Ă��܂�(�ʐς����߂�
�̈ʒu�W��}������ƉE�}�̂悤�ɂȂ��Ă��܂�(�ʐς����߂�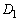 �C
�C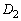 �̋��ʕ����͉��ΐF���F��)�B
�̋��ʕ����͉��ΐF���F��)�B
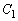 �C
�C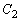 ������
������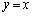 �Ɋւ��đΏ̂Ȃ̂ŁA
�Ɋւ��đΏ̂Ȃ̂ŁA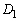 �C
�C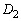 �̋��ʕ���������
�̋��ʕ���������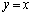 �Ɋւ��đΏ̂ŁA���߂��ʐ��́A����
�Ɋւ��đΏ̂ŁA���߂��ʐ��́A����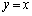 �ƁA
�ƁA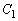 ��
��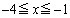 �̕����ƁA
�̕����ƁA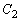 ��
��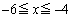 �̕����A�Ɉ͂܂ꂽ�����̖ʐ�S��2�{�ɂȂ�܂��B
�̕����A�Ɉ͂܂ꂽ�����̖ʐ�S��2�{�ɂȂ�܂��B
�����ŁA�ɗ́A��L�̌���(��)��p���ĊȒP�Ȍv�Z�ʼn��邱�Ƃ�ڎw���܂��B
����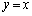 (�E�}�ΐF�̒���)��
(�E�}�ΐF�̒���)��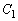 �ň͂܂�镔��(
�ň͂܂�镔��(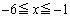 �͈̔͂ɑ��݂��܂�)�̖ʐς�
�͈̔͂ɑ��݂��܂�)�̖ʐς�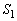 �C
�C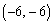 ��
��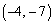 �����Ԓ���
�����Ԓ���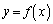 (�E�}�F�̒���)��
(�E�}�F�̒���)��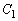 �ň͂܂�镔���̖ʐς�
�ň͂܂�镔���̖ʐς�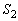 �C
�C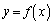 ��
��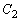 �ň͂܂�镔���̖ʐς�
�ň͂܂�镔���̖ʐς�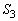 �Ƃ���ƁA
�Ƃ���ƁA
�ł��B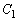 ��
��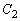 ������
������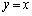 �Ɋւ��đΏ̂ł��邱�Ƃ���A
�Ɋւ��đΏ̂ł��邱�Ƃ���A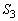 �́A
�́A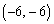 ��
��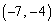 �����Ԓ���
�����Ԓ���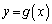 (�E�}�ԐF�̒���)��
(�E�}�ԐF�̒���)��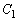 �ň͂܂�镔���̖ʐςɓ������A������̖ʐςƂ��Čv�Z���邱�Ƃɂ��܂��B
�ň͂܂�镔���̖ʐςɓ������A������̖ʐςƂ��Čv�Z���邱�Ƃɂ��܂��B
�� 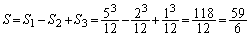
���߂�ʐς͂���2�{�ŁA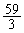 ......[��]
......[��]
�NjL�D����(��)�̎g�p���ד����Ƃ��āA���Ƃ���Ɍ����搶�����܂��B�ł����A�K������̂�����Ȍv�Z�Z�I�Ȃ�Ƃ������A�֗��Ɏg��������̎g�p�����������ד��ƌ����ׂ��ł��B'99�N�ɓ��傪���@�藝�̏ؖ����o�肵�܂������A����̑��ɂ��Ȃ�悤�ȏؖ�����X���Ȃ���Ή��@�藝���g���Ȃ��A�Ƃ����̂ł͉Ȋw�̐i���Ƀu���[�L��������悤�Ȃ��̂ł��B�l�ނ̐i���ƂƂ��Ɋm�����ꂽ�Ȋw�Z�p�̗����͋��ׂ��ł����āA����̂��߂ɓꕶ����l�̐��������ׂ����A�ȂǂƂ����̂̓i���Z���X�ł��B��l���n�ӍH�v���Â炵�O�����߂Đ���J�������`�������E�Ȋw�Z�p�͑f���Ɍp�����ĐϋɓI�ɗ��p����ׂ��ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B