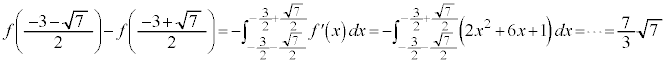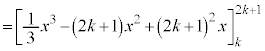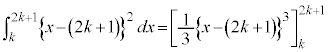��ϕ��̌����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂɂ��ẮA��ϕ��A��ϕ��Ɩʐ����Q�Ƃ��Ă��������B
(i) n����̎��R���̂Ƃ��A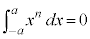
(ii) n�������̎��R���܂���0�̂Ƃ��A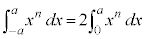
(iii) 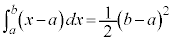 �C
�C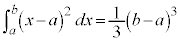 �C
�C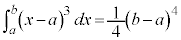
(iv) 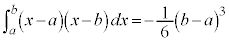
(v) 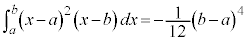
(vi) 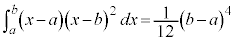
(vii) 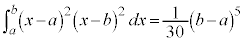
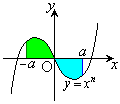 [�ؖ�](i)
[�ؖ�](i) 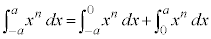
�E�}�Ő��F�̕����̐ϕ��͕��A���ΐF�̕����̐ϕ��͐��ŁA�������킹��Ƒł����������ă[���ɂȂ�܂��B
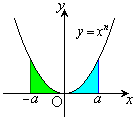 (ii)
(ii) 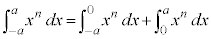
�E�}�Ő��F�̕����̐ϕ��ƁA���ΐF�̕����̐ϕ��͓������A�������킹��ƁA���F�̕����̐ϕ���2�{�ɂȂ�܂��B
(iii) 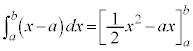
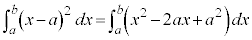
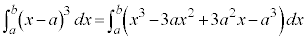
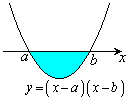 (iv)
(iv) 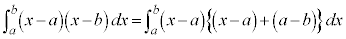
���̒�ϕ��́A�E�}�̐��F�̕����A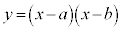 ��x���Ƃň͂ޕ����̖ʐςɑΉ����Ă��܂��B�ϕ���Ԃ�
��x���Ƃň͂ޕ����̖ʐςɑΉ����Ă��܂��B�ϕ���Ԃ�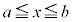 �ɂ����ẮA�Ȑ���x�����牺���ɂ���̂Œ�ϕ��̒l�͕��ɂȂ�܂��B
�ɂ����ẮA�Ȑ���x�����牺���ɂ���̂Œ�ϕ��̒l�͕��ɂȂ�܂��B
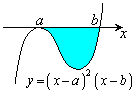 (v)
(v) 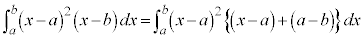
���̒�ϕ��́A�E�}�̐��F�̕����A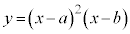 ��x���ň͂ޕ����̖ʐςɑΉ����Ă��܂��B�ϕ���Ԃ�
��x���ň͂ޕ����̖ʐςɑΉ����Ă��܂��B�ϕ���Ԃ� �ɂ����ẮA�Ȑ���x�����牺���ɂ���̂Œ�ϕ��̒l�͕��ɂȂ�܂��B
�ɂ����ẮA�Ȑ���x�����牺���ɂ���̂Œ�ϕ��̒l�͕��ɂȂ�܂��B
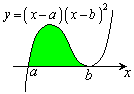 (vi)
(vi) 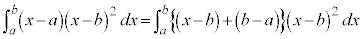
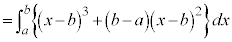
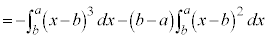 �@(�ϕ���Ԃ̏�[�Ɖ��[���t�ɂ���)
�@(�ϕ���Ԃ̏�[�Ɖ��[���t�ɂ���)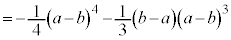
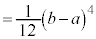
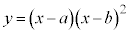 ��x���ň͂ޕ����̖ʐςɑΉ����Ă��܂��B�ϕ���Ԃ�
��x���ň͂ޕ����̖ʐςɑΉ����Ă��܂��B�ϕ���Ԃ�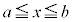 �ɂ����ẮA�Ȑ���x������㑤�ɂ���̂Œ�ϕ��̒l�͐��ɂȂ�܂��B
�ɂ����ẮA�Ȑ���x������㑤�ɂ���̂Œ�ϕ��̒l�͐��ɂȂ�܂��B
(�ؖ��I)
(vii) �����ϕ��@��p���ďؖ����܂��B
��1�D 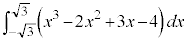
��L�̒�ϕ��̌���(i)�C(ii)���A��ϕ����F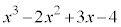 �̊���̍��̌v�Z�͕s�v(�ǂ����[���ɂȂ�)�ŁA�������̍��ɂ��ẮA
�̊���̍��̌v�Z�͕s�v(�ǂ����[���ɂȂ�)�ŁA�������̍��ɂ��ẮA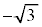 ����
����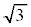 �܂ł̐ϕ��͈͂��A0����
�܂ł̐ϕ��͈͂��A0����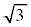 �܂łɕς������(��[�A���[�̂����ꂩ��0�ɂ��邾���ł��A���Ƃ�0��������Ƃ��Ɍv�Z�̎�Ԃ����Ȃ�y�������)2�{���܂��B�������āA
�܂łɕς������(��[�A���[�̂����ꂩ��0�ɂ��邾���ł��A���Ƃ�0��������Ƃ��Ɍv�Z�̎�Ԃ����Ȃ�y�������)2�{���܂��B�������āA
��2�D 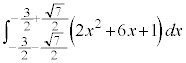
���̒�ϕ��̌v�Z���A
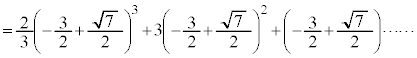 �@����@
�@����@
��ϕ��̏�[�Ɖ��[�́A��ϕ�����0�Ƃ��Ăł���2��������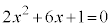 �̉�
�̉�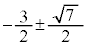 �Ȃ̂ŁA��L�̒�ϕ��̌���(iv)�𗘗p���āB
�Ȃ̂ŁA��L�̒�ϕ��̌���(iv)�𗘗p���āB
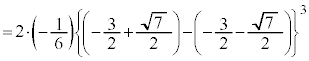
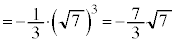 �@����A
�@����A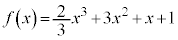 �̋ɑ�l�Ƌɏ��l�̍������߂�A�Ƃ������ɂ��g���܂��B�ɑ�l�Ƌɏ��l�����߂邽�߂ɁA
�̋ɑ�l�Ƌɏ��l�̍������߂�A�Ƃ������ɂ��g���܂��B�ɑ�l�Ƌɏ��l�����߂邽�߂ɁA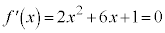 �������āA
�������āA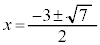 ���A
���A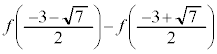 ���@�̂悤�Ɍv�Z����̂ł͑�ςł��B�����ŁA��ϕ��̌���(iv)��p���āA��L�A�̂悤�ɂ���A
���@�̂悤�Ɍv�Z����̂ł͑�ςł��B�����ŁA��ϕ��̌���(iv)��p���āA��L�A�̂悤�ɂ���A
�Ƃ��āA���N�Ɍv�Z���邱�Ƃ��ł��܂��B
��3�D 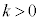 �Ƃ���B�Ȑ��F
�Ƃ���B�Ȑ��F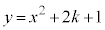 ��x����̓_
��x����̓_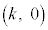 ���������2�{�̐ڐ��̂����A�ړ_��x���W�����̂��̂ƁA���̋Ȑ��ƒ����F
���������2�{�̐ڐ��̂����A�ړ_��x���W�����̂��̂ƁA���̋Ȑ��ƒ����F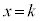 �Ƃň͂܂�镔���̖ʐς����߂�B
�Ƃň͂܂�镔���̖ʐς����߂�B
[��]�@�Ȑ��F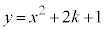 �@����@
�@����@
�@���������āA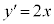
�ړ_��x���W��t�Ƃ��āA�ړ_��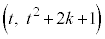 �C�ڐ��̌X����
�C�ڐ��̌X����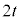
�ڐ��́A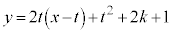
�������āA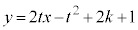 �@����A
�@����A
�A�́A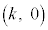 ��ʂ邩��A
��ʂ邩��A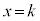 �C
�C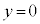 �������āA
�������āA
�� 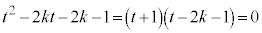
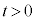 ���A
���A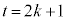 (
(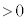 )
)
�A�ɑ�����āA�ڐ��̕������́A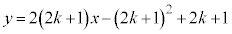
���߂��ʐ��́A�@����A�������āA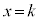 ����
����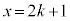 �܂Őϕ��������̂ɂȂ�܂��B������A
�܂Őϕ��������̂ɂȂ�܂��B������A
�Ƃ���Ă��܂��Ƒ������܂��B
��ϕ����́A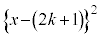 �ƈ��������ł��܂��B
�ƈ��������ł��܂��B
�Ƃ������A�@�ƇA�Ƃ́A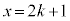 �Őڂ���̂ŁA�A������A
�Őڂ���̂ŁA�A������A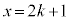 ���d���Ɏ����܂��B�@��
���d���Ɏ����܂��B�@��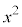 �̌W����1�Ȃ̂ŁA2�����@���\���Ȑ��Ɛڐ��Ƃň͂ޕ����̖ʐς��v�Z���悤�Ƃ���A
�̌W����1�Ȃ̂ŁA2�����@���\���Ȑ��Ɛڐ��Ƃň͂ޕ����̖ʐς��v�Z���悤�Ƃ���A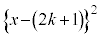 �̌`��ϕ����邱�ƂɂȂ�Ƃ����̂́A�ړ_�̍��W�����܂������_�ł킩���Ă��邱�Ƃł��B����āA���߂�ʐς́A��L�̒�ϕ��̌���(iii)��p���āA�ȉ��̂悤�Ɍv�Z���܂��B
�̌`��ϕ����邱�ƂɂȂ�Ƃ����̂́A�ړ_�̍��W�����܂������_�ł킩���Ă��邱�Ƃł��B����āA���߂�ʐς́A��L�̒�ϕ��̌���(iii)��p���āA�ȉ��̂悤�Ɍv�Z���܂��B
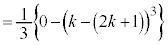
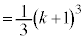 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 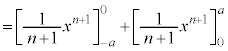
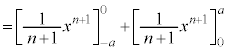
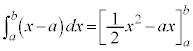
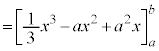
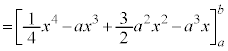
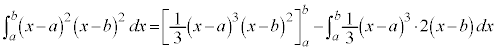
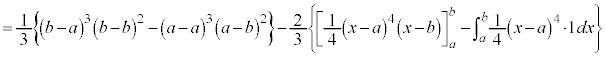
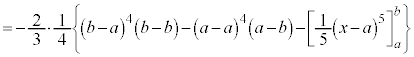
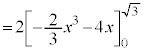
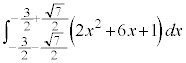
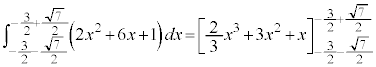
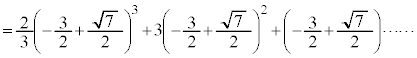 �@����@
�@����@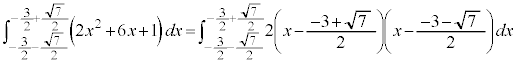
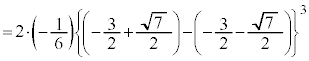
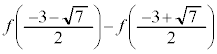 ���@�̂悤�Ɍv�Z����̂ł͑�ςł��B�����ŁA��ϕ��̌���(iv)��p���āA��L�A�̂悤�ɂ���A
���@�̂悤�Ɍv�Z����̂ł͑�ςł��B�����ŁA��ϕ��̌���(iv)��p���āA��L�A�̂悤�ɂ���A