��s�啶�n���w'10�N[3]
����a�Cb�Cc�Cd�ɑ�x��3���̐���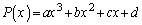 ���l����B�������A
���l����B�������A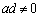 �Ƃ���B������
�Ƃ���B������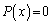 ��3�̉���α�Cβ�Cγ�Ƃ����
��3�̉���α�Cβ�Cγ�Ƃ����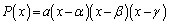 �ł��邱�Ƃ��m���Ă���B���̂Ƃ��A�ȉ��̖₢�ɓ�����B
�ł��邱�Ƃ��m���Ă���B���̂Ƃ��A�ȉ��̖₢�ɓ�����B
(1) ��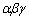 �C�a
�C�a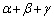 �C
�C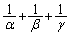 ���A���ꂼ��a�Cb�Cc�Cd��p���ĕ\���B
���A���ꂼ��a�Cb�Cc�Cd��p���ĕ\���B (2) ����α�������łȂ��Ȃ�A������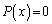 ��α�̋����ȕ��f��
��α�̋����ȕ��f��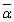 �����Ɏ����Ƃ��ؖ�����B
�����Ɏ����Ƃ��ؖ�����B (3) ��α�Cβ�Cγ�̂��������ƂȂ���̂̌���0�C1�C2�C3�̂ǂꂩ�B�l������\�������ׂāA���R���q�ׂē�����B
(4) �����A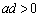 �Ȃ�A��α�Cβ�Cγ�̂������̎����ƂȂ���̂̌���0�C1�C2�C3�̂ǂꂩ�B�l������\�������ׂāA���R���q�ׂē�����B
�Ȃ�A��α�Cβ�Cγ�̂������̎����ƂȂ���̂̌���0�C1�C2�C3�̂ǂꂩ�B�l������\�������ׂāA���R���q�ׂē�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@3�����������e�[�}�̖��ł��B�Ȃ��A�������������Q�Ƃ��Ă��������B
(1) 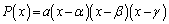
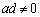 ���A
���A
(2) α�������łȂ��̂ŁA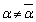 �ł��B
�ł��B ����āA
����āA������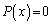 ��
��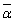 �����Ɏ����܂��B
�����Ɏ����܂��B
(3) α�Cβ�Cγ�������ł���A�@���A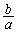 �C
�C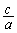 �C
�C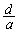 �������Ȃ̂ŁA�������̌���3�ƂȂ�ꍇ������܂��B
�������Ȃ̂ŁA�������̌���3�ƂȂ�ꍇ������܂��B (2)���A�����łȂ���α��1���ƁA�������f��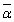 (
(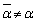 )�����ɂȂ�̂ŁA�����łȂ�����1�A�܂�A�������̌���2�Ƃ������Ƃ͂��蓾�܂���B
)�����ɂȂ�̂ŁA�����łȂ�����1�A�܂�A�������̌���2�Ƃ������Ƃ͂��蓾�܂���B
�@�ŁA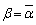 ���Ƃ���ƁA
���Ƃ���ƁA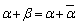 �C
�C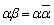 �͎����Ȃ̂ŁA�@���
�͎����Ȃ̂ŁA�@��� �ł����āAγ�͎����ł��B�]���āA�������̌���1�ƂȂ�ꍇ������܂��B
�܂��A�����łȂ���α��1���Ƃ��A����ȊO�ɁA�����łȂ���γ (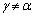 )�����ƁA���̋��f��
)�����ƁA���̋��f��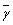 �����łȂ���Ȃ炸�A
�����łȂ���Ȃ炸�A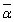 �����Ȃ̂ŁA
�����Ȃ̂ŁA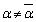 �C
�C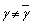 ���A3���������̉���4�Ƃ������ƂɂȂ��Ă��܂��܂��B����āA�������̌���0�Ƃ������Ƃ͂��蓾�܂���B
���A3���������̉���4�Ƃ������ƂɂȂ��Ă��܂��܂��B����āA�������̌���0�Ƃ������Ƃ͂��蓾�܂���B
�ȏ���A�������̌���1�C�܂���3 ......[��]�@�ł��B
(4) 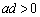 �Ȃ̂�a�Cd�͓������ŁA(1)�̌��ʂ��
�Ȃ̂�a�Cd�͓������ŁA(1)�̌��ʂ��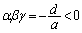 �ł��B
�ł��B α�Cβ�Cγ�̒��Ɏ����łȂ����̂�����Ƃ��Aα�������łȂ��Ƃ��āA(2)���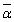 �����ł����A
�����ł����A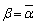 ���Ƃ���ƁA
���Ƃ���ƁA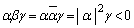 (��Βl���Q��)���
(��Βl���Q��)���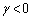 �Ő��̎������͂���܂���Bα�Cβ�Cγ��3�Ƃ������ł���A
�Ő��̎������͂���܂���Bα�Cβ�Cγ��3�Ƃ������ł���A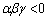 ���Aα�Cβ�Cγ��3�Ƃ����A�܂��́A1������2�����̂����ꂩ�ł��B
���Aα�Cβ�Cγ��3�Ƃ����A�܂��́A1������2�����̂����ꂩ�ł��B
�]���āA���̎����ƂȂ���̂̌��́A0�܂���2 ......[��]�@�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 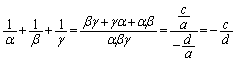 ......[��]
......[��]