�����������@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
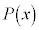 ��x�Ɋւ���n�������������Ƃ��āA
��x�Ɋւ���n�������������Ƃ��āA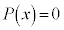 ��n���������ƌ����B
��n���������ƌ����B
3���ȏ�̕���������ɁA�����������ƌĂԁB
���R��n�ɑ��āA���f���W����n�������������f���͈̔͂ɏ��Ȃ��Ƃ�1�̉���L���邱�Ƃ��K�E�X�ɂ��ؖ�����Ă��܂��B
���̎������g���ƁAn��������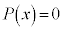 �����f��
�����f��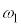 �����Ɏ��ĂA
�����Ɏ��ĂA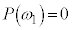 �Ȃ̂ŁA�����藝���A
�Ȃ̂ŁA�����藝���A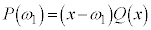 �ƈ��������ł��܂��B
�ƈ��������ł��܂��B
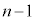 ��������
��������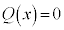 �����l�ɕ��f���͈̔͂ɏ��Ȃ��Ƃ�1�̉�
�����l�ɕ��f���͈̔͂ɏ��Ȃ��Ƃ�1�̉�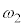 �����̂ŁA
�����̂ŁA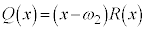 �ƈ��������ł��܂��B
�ƈ��������ł��܂��B
������J��Ԃ��Ă䂯�A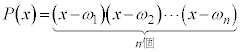 �̌`�Ɉ�����������āAn�������������f���͈̔͂�n�̉��A
�̌`�Ɉ�����������āAn�������������f���͈̔͂�n�̉��A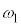 �C
�C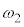 �C����C
�C����C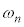 �������Ƃ��킩��܂��B
�������Ƃ��킩��܂��B
���̎����́A�����ł͊��m�Ƃ��ėǂ��ł��傤�B
n����������n�̉��̒��ɂ́A��v���Ă��܂����̂��o�Ă��邱�Ƃ�����܂��B
�قȂ�i�Cj (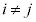 �C
�C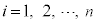 �C
�C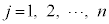 )�ɂ��āA
)�ɂ��āA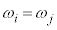 �ƂȂ��������A�����2�d���ƌ����܂��B
�ƂȂ��������A�����2�d���ƌ����܂��B
�قȂ�i�Cj�Ck (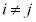 �C
�C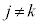 �C
�C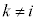 �C
�C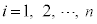 �C
�C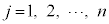 �C
�C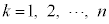 )�ɂ��āA
)�ɂ��āA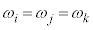 �ƂȂ��������A�����3�d���ƌ����܂��B
�ƂȂ��������A�����3�d���ƌ����܂��B
�����W����n���������F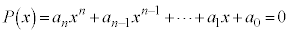 (
(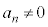 �C
�C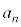 �C
�C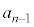 �C����C
�C����C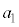 �C
�C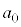 �͎���)��������z�����Ƃ���ƁA
�͎���)��������z�����Ƃ���ƁA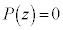
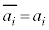 (
(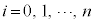 )���(���f�����Q��)�A
)���(���f�����Q��)�A
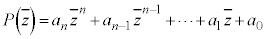
�@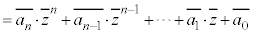
�@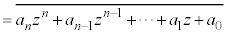
�@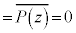
�܂�A�����W����n���������F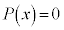 ��������z�����ĂA
��������z�����ĂA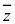 ���܂����ɂȂ�܂��B
���܂����ɂȂ�܂��B
�ȉ��Ai�������P�ʂƂ��āA2���������F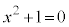 �̉��́A
�̉��́A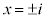
2���������F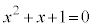 �̉��́A
�̉��́A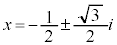
2���������F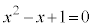 �̉��́A
�̉��́A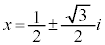
3���������F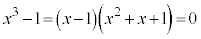 �̉��́A
�̉��́A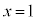 �C
�C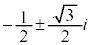
3���������F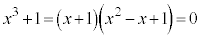 �̉��́A
�̉��́A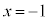 �C
�C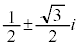
��Da�Cb�͎������Ƃ���B4���������F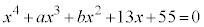 ���A
���A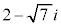 �����Ɏ��Ƃ��Aa�Cb�̒l���߂āA�c��̉������߂�B
�����Ɏ��Ƃ��Aa�Cb�̒l���߂āA�c��̉������߂�B
[��]�@�����W����4���������Ȃ̂ŁA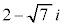 �����Ɏ��ĂA
�����Ɏ��ĂA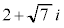 �����ɂȂ�܂��B
�����ɂȂ�܂��B
2���̘a�F4�C2���̐ρF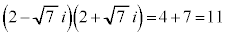 �C���ƌW���̊W���A
�C���ƌW���̊W���A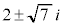 �����Ɏ���2���������́A
�����Ɏ���2���������́A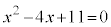 ����@ �ł��B
����@ �ł��B
4���������̒萔����55�ŁA�@�̒萔����11�Ȃ̂ŁA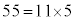 ���A4���������̍��ӂ́A
���A4���������̍��ӂ́A
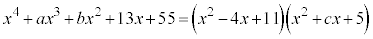 ����A
����A
�ƈ��������ł���͂��ł��B
�A�̉E�ӂ�W�J�����Ƃ���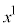 �̍��́A
�̍��́A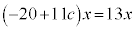 �ƂȂ�͂��ł��B
�ƂȂ�͂��ł��B
�� 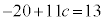
�� 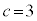
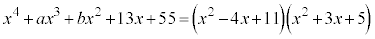
�@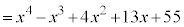
���A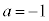 �C
�C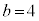 ......[��]
......[��]
�܂��A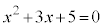 �̉��́A
�̉��́A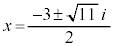
���߂�c��̉��́A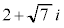 �C
�C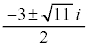 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 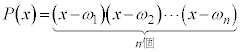 �̌`�Ɉ�����������āAn�������������f���͈̔͂�n�̉��A
�̌`�Ɉ�����������āAn�������������f���͈̔͂�n�̉��A