��嗝�n���w'10�N�O��[2]
 �Ƃ���B2�̋Ȑ�
�Ƃ���B2�̋Ȑ�
�̌�_�̂����Ax���W��y���W���Ƃ��ɐ��ł�����̂�P�Ƃ���BP�ɂ�����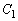 �C
�C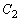 �̐ڐ������ꂼ��
�̐ڐ������ꂼ�� �C
�C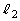 �Ƃ��Ay����
�Ƃ��Ay���� �C
�C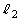 �̌�_�����ꂼ��Q�CR�Ƃ���Bθ ��
�̌�_�����ꂼ��Q�CR�Ƃ���Bθ �� �͈̔͂��Ƃ��A����QR�̒����̍ŏ��l�����߂�B
�͈̔͂��Ƃ��A����QR�̒����̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2���Ȑ��̊�{���ł����A�����I�ɂ͎O�p���̌v�Z���ł��B
 �F
�F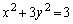 �@����@�@(�ȉ~���Q��)
�@����@�@(�ȉ~���Q��)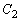 �F
�F �@����A�@(�o�Ȑ����Q��)
�@����A�@(�o�Ȑ����Q��)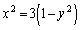 �@����B
�@����B
�A�ɑ�����āA
�� 
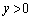 �C
�C ���A
���A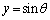
�B�ɑ�����āA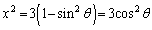
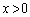 �C
�C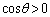 ���A
���A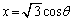
������P�̍��W�́A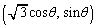
�_P�ɂ�����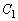 �̐ڐ��́A
�̐ڐ��́A
 �F
�F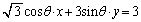
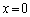 �Ƃ���ƁA
�Ƃ���ƁA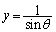
����āAQ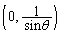
�_P�ɂ�����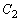 �̐ڐ��́A
�̐ڐ��́A
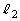 �F
�F
 �Ƃ���ƁA
�Ƃ���ƁA
����āAR
����QR�̒����́A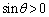 ���������ρE���敽�ς̊W���A
���������ρE���敽�ς̊W���A
�s�����̓�������������̂́A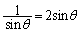 �C�܂�A
�C�܂�A �C
�C �C
�C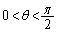 ���A
���A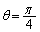 �̂Ƃ��B
�̂Ƃ��B
����QR�̒����̍ŏ��l��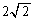 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 