��嗝�n���w'10�N���[4]
�~C�́A2�̕�����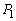 �F
�F (
( )��
)�� �F
�F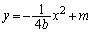 (
(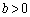 �C
�C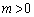 )�ň͂܂ꂽ�̈���ɂ���A�����̕������Ƌ��L�_�������A�����y����ɒ��S�����Ƃ���B���̂Ƃ��A�ȉ��̂��Ƃ������B
)�ň͂܂ꂽ�̈���ɂ���A�����̕������Ƌ��L�_�������A�����y����ɒ��S�����Ƃ���B���̂Ƃ��A�ȉ��̂��Ƃ������B
(1) C��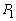 �����
����� �̂��ꂼ���1�_�݂̂����L����Ȃ�A
�̂��ꂼ���1�_�݂̂����L����Ȃ�A ����
����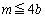 �ł���B
�ł���B (2) C��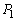 �����
����� �̂��ꂼ���2�_�����L����Ȃ�A
�̂��ꂼ���2�_�����L����Ȃ�A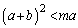 ����
����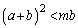 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�~�ƕ������̈ʒu�W�̖��Ȃ̂ł����A����2�����������l���邱�ƂɂȂ�܂��B
(1) �~C�A������ �C
�C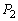 ��y���Ɋւ��đΏ̂Ȃ̂ŁAC��
��y���Ɋւ��đΏ̂Ȃ̂ŁAC��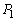 �����L�_�����Ƃ�
�����L�_�����Ƃ� �ɂ����ċ��L�_�����ĂAy���Ɋւ��Ă��̋��L�_�ƑΏ̂ȓ_���܂����L�_�ƂȂ�A���L�_�͏��Ȃ��Ƃ�2����܂��BC��
�ɂ����ċ��L�_�����ĂAy���Ɋւ��Ă��̋��L�_�ƑΏ̂ȓ_���܂����L�_�ƂȂ�A���L�_�͏��Ȃ��Ƃ�2����܂��BC��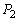 �����l�ł��B
�����l�ł��B �]���āAC��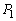 ��1�_�݂̂����L����̂ł���A���̋��L�_��y����̓_�ł���A������
��1�_�݂̂����L����̂ł���A���̋��L�_��y����̓_�ł���A������ �̒��_
�̒��_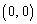 �ł��B���l�ɁAC��
�ł��B���l�ɁAC��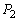 ��1�_�݂̂����L����̂ł���A���̋��L�_��y����̓_��
��1�_�݂̂����L����̂ł���A���̋��L�_��y����̓_��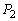 �̒��_
�̒��_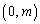 �ł��B�Ƃ������Ƃ́A�~C�́A2�_
�ł��B�Ƃ������Ƃ́A�~C�́A2�_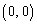 �C
�C �a�̗��[�Ƃ���~�ŁA���S
�a�̗��[�Ƃ���~�ŁA���S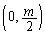 �C���a
�C���a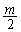 �̉~���Ƃ������Ƃł��B�~C���������́A
�̉~���Ƃ������Ƃł��B�~C���������́A �ƘA������ƁA
�� 
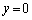 �̂Ƃ�
�̂Ƃ�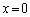 �ł��B
�ł��B
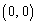 �ȊO�ɋ��L�_�͂Ȃ��̂ŁA
�ȊO�ɋ��L�_�͂Ȃ��̂ŁA ��x�̕������Ƃ��ĉ��������Ȃ����A���邢�́A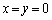 �����ɂȂ�悢�̂ŁA
�����ɂȂ�悢�̂ŁA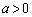 ���A
���A  �@��
�@��  �@����A
�@����A�@�ƁA �F
�F ��A������ƁA
��A������ƁA �� 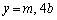
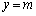 �̂Ƃ�
�̂Ƃ� �ł��B
�ł��B
 �ȊO�ɋ��L�_�͂Ȃ��̂ŁA
�ȊO�ɋ��L�_�͂Ȃ��̂ŁA �����������Ȃ����A���邢�́A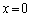 �C
�C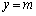 �����ɂȂ�悢�̂ŁA
�����ɂȂ�悢�̂ŁA ���A
���A  �@��
�@�� 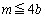 �@����B
�@����B�A�C�B���AC��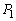 �����
�����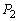 �̂��ꂼ���1�_�݂̂����L����Ȃ�A
�̂��ꂼ���1�_�݂̂����L����Ȃ�A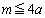 ����
����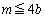 �ł��B
�ł��B
(2) (1)�Ɠ��l�ɍl���܂��BC��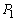 �C
�C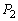 ��y���Ɋւ��đΏ̂ł��邱�Ƃ���AC��
��y���Ɋւ��đΏ̂ł��邱�Ƃ���AC��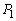 �����L�_��2�_���̂ł���A����2�_��y���Ɋւ��đΏ̂�y���W�͋��ʂł��B�܂��A2���L�_�͐ړ_�ŁA����x���W�͐�Βl���������������قȂ�܂��B���l��C��
�����L�_��2�_���̂ł���A����2�_��y���Ɋւ��đΏ̂�y���W�͋��ʂł��B�܂��A2���L�_�͐ړ_�ŁA����x���W�͐�Βl���������������قȂ�܂��B���l��C�� �����L�_��2�_���̂ł���A����2�_��y���Ɋւ��đΏ̂�y���W�͋��ʂł��B��������A2���L�_�͐ړ_�ŁA����x���W�͐�Βl���������������قȂ�܂��B
�����L�_��2�_���̂ł���A����2�_��y���Ɋւ��đΏ̂�y���W�͋��ʂł��B��������A2���L�_�͐ړ_�ŁA����x���W�͐�Βl���������������قȂ�܂��B �~C�̒��S��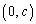 �C���a��r�Ƃ��āA�~C�̕��������A
�C���a��r�Ƃ��āA�~C�̕��������A 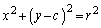
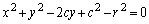 �@����C
�@����C�Ƃ��܂��B
 �F
�F
�ƘA������ƁA
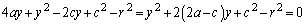 �@����D
�@����D�d�������̂ŁA���ʎ� �ɂ��āA
�ɂ��āA ���̏������ɇE�̏d���́A
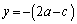 �@����F
�@����F�C�ƁA �F
�F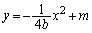 ��A������ƁA
��A������ƁA 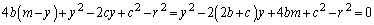 �@����G
�@����G�d�������̂ŁA���ʎ� �ɂ��āA
�ɂ��āA  �@����H
�@����H���̏������ɇG�̏d���́A
 �@����I
�@����I�F�C�I�ɕ���c�������Ă���̂ŁAc�����߂܂��B
�E�|�H���A
��  �F���A
�F���A ���̂Ƃ��A �̕��������A
�̕��������A ���ꂪ�A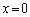 �ȊO��2���������߂ɁA
�ȊO��2���������߂ɁA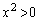 �C
�C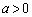 �C
�C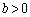 ���A
���A 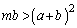 �@����J
�@����J�I���A
���̂Ƃ��A �̕��������A
�̕��������A ���ꂪ�A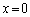 �ȊO��2���������߂ɁA
�ȊO��2���������߂ɁA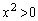 �C
�C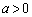 �C
�C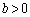 ���A
���A 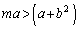 �@����K
�@����K�J�C�K���AC��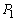 �����
����� �̂��ꂼ���2�_�����L����Ȃ�A
�̂��ꂼ���2�_�����L����Ȃ�A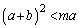 ����
����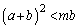 �ł��B
�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B