��吔�w'10�N���[4]
�\�Ɨ��̏o��m����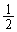 ���̍d�݂𓊂��A�\�Ȃ�1�_�A���Ȃ�0�_�Ƃ���Bk�Cn�𐳂̐����Ƃ��āA�ȉ��̖₢�ɓ�����B
���̍d�݂𓊂��A�\�Ȃ�1�_�A���Ȃ�0�_�Ƃ���Bk�Cn�𐳂̐����Ƃ��āA�ȉ��̖₢�ɓ�����B
1�D�d�݂��J��Ԃ��ē����A���_�̍��v��3�_�ɒB������I�����邱�Ƃɂ���B���傤��5��ڂŏI������m���͂����炩�B�܂��A���傤��n��ڂŏI������m����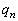 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A ���ؖ�����B
���ؖ�����B 2�D�d�݂��J��Ԃ��ē����A���_�̍��v��k�_�ɒB������I�����邱�Ƃɂ���B���傤��n��ڂŏI������m����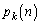 �Ƃ���Bk���Œ肵���܂�n�����Ƃ���
�Ƃ���Bk���Œ肵���܂�n�����Ƃ���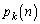 �̍ő�l�����߂�B
�̍ő�l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������s�̖��ł��B1��̎��s�Ŏ���A�̋N����m����p�̂Ƃ��An��̎��s��k��A���N����m���� �ɂȂ�A�Ƃ����A�������s�̌������g���ĉ��܂��傤�B
�ɂȂ�A�Ƃ����A�������s�̌������g���ĉ��܂��傤�B
1�D���傤��5��ŏI������̂́A4��ڂ܂łɁA�\��2��A����2��o��(�m��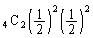 )���āA5��ڂɕ\���o��(�m��
)���āA5��ڂɕ\���o��(�m��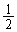 )�Ƃ��ł��B���̊m���́A
)�Ƃ��ł��B���̊m���́A  ......[��]
......[��]3��ȏ㓊���Ȃ��Ɠ��_��3�_�ɂȂ�Ȃ��̂ŁA �ł��B
�ł��B
 �̂Ƃ��A���傤��n��ڂœ��_�̍��v��3�_�ɂȂ�̂́A
�̂Ƃ��A���傤��n��ڂœ��_�̍��v��3�_�ɂȂ�̂́A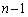 ��ڂ܂łɁA�\��2��A����
��ڂ܂łɁA�\��2��A���� ��o��(�m��
��o��(�m��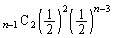 )���āAn��ڂɕ\���o��(�m��
)���āAn��ڂɕ\���o��(�m��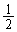 )�Ƃ��ł��B���̊m��
)�Ƃ��ł��B���̊m��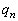 �́A
�́A ������g���āA ���v�Z����̂̓L�r�����̂ŁA�ؖ����ׂ����̌`����A�]�������l���邱�Ƃɂ��܂��B
���v�Z����̂̓L�r�����̂ŁA�ؖ����ׂ����̌`����A�]�������l���邱�Ƃɂ��܂��B
�m���� �ƂȂ�̂́An��ڂ܂łɏI������A�Ƃ������ۂł��B���̗]���ۂ́An��ڂ܂łɏI�����Ȃ��A�܂�An��d�݂𓊂��āA�\�̏o����0��1��2��A�Ƃ������ۂł��Bn��d�ݓ������s���āA�\��0��ƂȂ�m���́A
�ƂȂ�̂́An��ڂ܂łɏI������A�Ƃ������ۂł��B���̗]���ۂ́An��ڂ܂łɏI�����Ȃ��A�܂�An��d�݂𓊂��āA�\�̏o����0��1��2��A�Ƃ������ۂł��Bn��d�ݓ������s���āA�\��0��ƂȂ�m���́A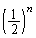 �C�\��1��ƂȂ�m���́A
�C�\��1��ƂȂ�m���́A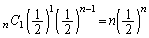 �C�\��2��ƂȂ�m���́A
�C�\��2��ƂȂ�m���́A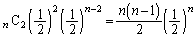
����āA�]���ۂ̊m���́A ����āAn��ڂ܂łɏI������m�� �́A
�́A 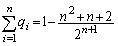 �@(�ؖ��I)
�@(�ؖ��I)
2�D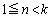 �̂Ƃ��́An��d�݂𓊂��Ă����_��k�_�ɂȂ邱�Ƃ͂Ȃ��̂ŁA
�̂Ƃ��́An��d�݂𓊂��Ă����_��k�_�ɂȂ邱�Ƃ͂Ȃ��̂ŁA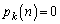 �ł��B
�ł��B  �̂Ƃ��A���傤��n��d�݂𓊂��ē��_��k�_�ƂȂ��ďI������̂́A
�̂Ƃ��A���傤��n��d�݂𓊂��ē��_��k�_�ƂȂ��ďI������̂́A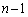 ��ڂ܂łɁA�\��
��ڂ܂łɁA�\��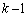 ��A����
��A����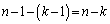 ��o��(�m��
��o��(�m�� )�An��ڂɕ\���o��(�m��
)�An��ڂɕ\���o��(�m��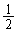 )�Ƃ��ŁA���̊m��
)�Ƃ��ŁA���̊m��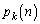 �́A
�́A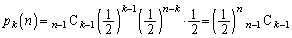 �@(�������A
�@(�������A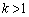 )�@����@
)�@����@(i)  �̂Ƃ��́A���傤��n��d�݂𓊂��ē��_��k�_�ƂȂ��ďI������̂́A1��ڂ���
�̂Ƃ��́A���傤��n��d�݂𓊂��ē��_��k�_�ƂȂ��ďI������̂́A1��ڂ��� ��ڂ܂ŗ����o��n��ڂɕ\���o��ꍇ�ŁA���̊m���́A
��ڂ܂ŗ����o��n��ڂɕ\���o��ꍇ�ŁA���̊m���́A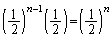
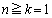 �̂Ƃ��A
�̂Ƃ��A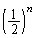 �́A
�́A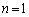 �̂Ƃ��ő�l
�̂Ƃ��ő�l ���Ƃ�܂��B
���Ƃ�܂��B(ii) 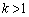 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A  �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA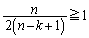
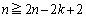 �C
�C �C������A
�C������A
 �̂Ƃ��A
�̂Ƃ��A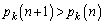
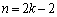 �̂Ƃ��A
�̂Ƃ��A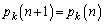
 �̂Ƃ��A
�̂Ƃ��A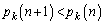
��  ������A
������A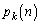 �́A
�́A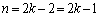 �̂Ƃ��A�ő�l
�̂Ƃ��A�ő�l���Ƃ�܂��B
(i)�C(ii)���A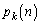 �̍ő�l�́A
�̍ő�l�́A
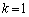 �̂Ƃ�
�̂Ƃ�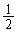 �C
�C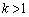 �̂Ƃ�
�̂Ƃ�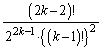 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 

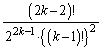 ......[��]
......[��]