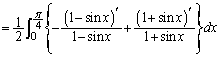�D�y��吔�w'10�N[4]
����n�ɑ��āA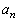 �������Œ�`����B
�������Œ�`����B
(1)  �C
�C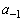 �����߂�B
�����߂�B (2) 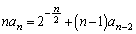 �����藧���Ƃ������B
�����藧���Ƃ������B (3) 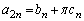 (������
(������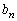 �C
�C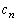 �͗L����)�ƕ\����邱�Ƃ������B�܂�
�͗L����)�ƕ\����邱�Ƃ������B�܂� �̂Ƃ���
�̂Ƃ���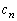 �����߂�B�K�v�Ȃ��π���������ł��邱�Ƃ�p���Ă悢�B
�����߂�B�K�v�Ȃ��π���������ł��邱�Ƃ�p���Ă悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�C(2)�͂悭����ϕ��v�Z���(�O�p���̐ϕ����Q��)�ł����A(3)���ϑ��I�����w�I�A�[�@�ɂȂ�܂��B
(1) 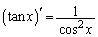 ���A
���A  ......[��]
......[��]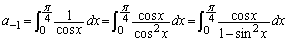
(2) 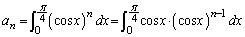
�� 
(�T)  �̂Ƃ��A(1)���A
�̂Ƃ��A(1)���A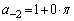
����āA (�L����)�C
(�L����)�C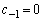 (�L����)�Ƃ���A
(�L����)�Ƃ���A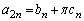 (������
(������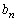 �C
�C �͗L����)�ƕ\����܂��B
�͗L����)�ƕ\����܂��B (�U)  �̂Ƃ��A
�̂Ƃ��A (������
(������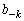 �C
�C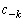 �͗L����)�ƕ\�����Ƃ��܂��B
�͗L����)�ƕ\�����Ƃ��܂��B (2)�ɂ����āA �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A  (�L����)�C
(�L����)�C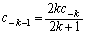 (�L����)�@����@
(�L����)�@����@�Ƃ��邱�Ƃɂ��A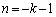 �̂Ƃ��ɂ��A
�̂Ƃ��ɂ��A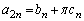 (������
(������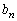 �C
�C �͗L����)�ƕ\����܂��B
�͗L����)�ƕ\����܂��B (�T)�C(�U)���An�����̐����̂Ƃ��A (������
(������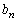 �C
�C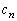 �͗L����)�ƕ\����܂��B
�͗L����)�ƕ\����܂��B
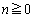 �̂Ƃ��ׂ܂��B
�̂Ƃ��ׂ܂��B (�T) 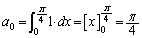
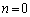 �̂Ƃ��A
�̂Ƃ��A (�L����)�C
(�L����)�C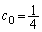 (�L����)�Ƃ���A
(�L����)�Ƃ���A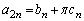 (������
(������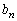 �C
�C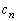 �͗L����)�ƕ\����܂��B
�͗L����)�ƕ\����܂��B(�U) 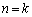 �̂Ƃ��A
�̂Ƃ��A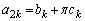 (������
(������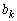 �C
�C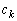 �͗L����)�ƕ\�����Ƃ��܂��B
�͗L����)�ƕ\�����Ƃ��܂��B (2)�ɂ����āA �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A 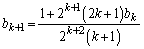 (�L����)�C
(�L����)�C (�L����)
(�L����)�Ƃ��邱�Ƃɂ��A �̂Ƃ��ɂ��A
�̂Ƃ��ɂ��A (������
(������ �C
�C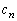 �͗L����)�ƕ\����܂��B
�͗L����)�ƕ\����܂��B (�T)�C(�U)���An��0�ȏ�̐����̂Ƃ��A (������
(������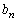 �C
�C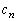 �͗L����)�ƕ\����܂��B
�͗L����)�ƕ\����܂��B
�@���J��Ԃ��p���邱�Ƃɂ��A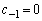 �䂦�A
�䂦�A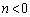 �̂Ƃ��A
�̂Ƃ��A ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B