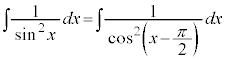三角関数の積分 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目は、不定積分の公式、置換積分、定積分の漸化式を参照してください。
三角関数のべき乗の積分の方法を整理しておきます。
不定積分で、例示しますが、定積分でも変わりはありません。
例1. 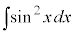 ,
,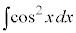
半角の公式を使います。
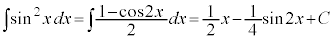 (C:積分定数)
(C:積分定数)
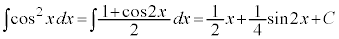 (C:積分定数)
(C:積分定数)
例2.  ,
,
被積分関数の中に、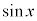 奇数個の積があるときには、
奇数個の積があるときには、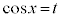 とおきます(置換積分を参照)。
とおきます(置換積分を参照)。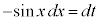 より、
より、
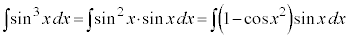
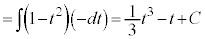
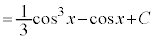 (C:積分定数)
(C:積分定数)
被積分関数の中に、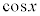 奇数個の積があるときには、
奇数個の積があるときには、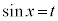 とおきます。
とおきます。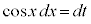
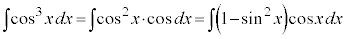
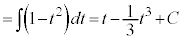
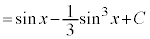 (C:積分定数)
(C:積分定数)
注.3倍角の公式の利用も考えられます。
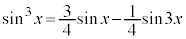 より、
より、
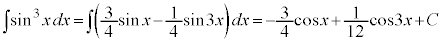 (C:積分定数)
(C:積分定数)
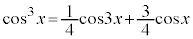 より、
より、
 (C:積分定数)
(C:積分定数)
例3. 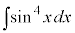 ,
,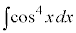
半角の公式を2回使います。

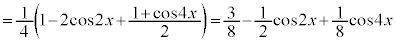 より、
より、
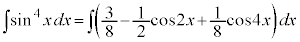
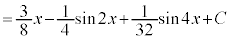 (C:積分定数)
(C:積分定数)
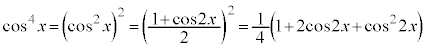
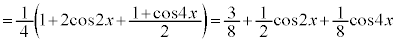 より、
より、
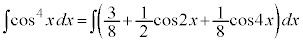
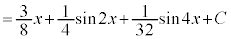 (C:積分定数)
(C:積分定数)
例4. 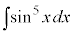 ,
,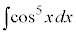
被積分関数の中に、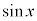 奇数個の積があるときには、
奇数個の積があるときには、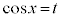 とおきます(置換積分を参照)。
とおきます(置換積分を参照)。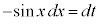 より、
より、
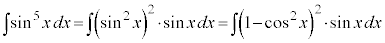

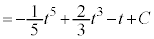
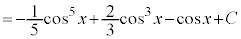 (C:積分定数)
(C:積分定数)
被積分関数の中に、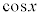 奇数個の積があるときには、
奇数個の積があるときには、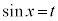 とおきます。
とおきます。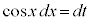
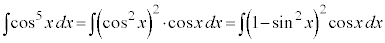
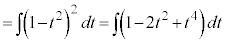
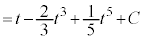
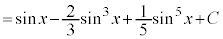 (C:積分定数)
(C:積分定数)
例5. 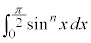 (
(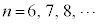 )
)
この形の積分が登場するのは、アステロイドの面積や体積を計算する場合なので、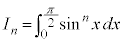 として、漸化式:
として、漸化式: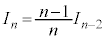 を利用するのがよいでしょう。なるべく、漸化式を暗記するのではなく、試験会場で漸化式を導く過程も答案に記して利用したいものです。
を利用するのがよいでしょう。なるべく、漸化式を暗記するのではなく、試験会場で漸化式を導く過程も答案に記して利用したいものです。
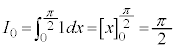 ,
,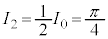 ,
,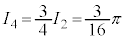 ,
, ,
, ,・・・
,・・・
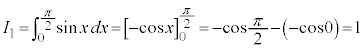 ,
,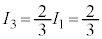 ,
,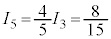 ,
,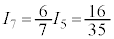 ,
,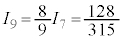 ,・・・
,・・・
なお、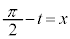 とおくと、
とおくと、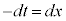 ,x:
,x: のとき、t:
のとき、t: より、
より、
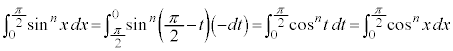
です。
例6. 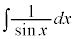 ,
,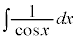
一番簡単なのは2倍角の公式を使う方法です。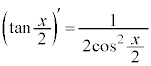 より、
より、
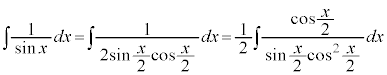
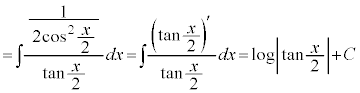 (C:積分定数)
(C:積分定数)
この方法は、わかりづらいので、あまりおすすめではありません。下記のようにするのがよいでしょう。
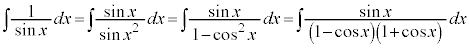
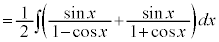
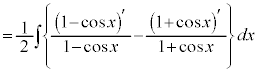
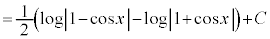
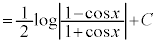 (C:積分定数)
(C:積分定数)
注.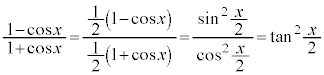 です。
です。
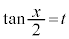 とおくと(置換積分を参照)、
とおくと(置換積分を参照)、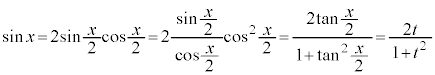 ,
,
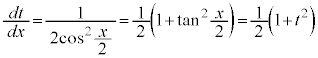 ,
,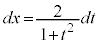 より、
より、
 (C:積分定数)
(C:積分定数)
とすることもできます。
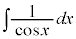 も、
も、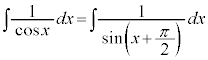 とすれば、上記と全く同じ考え方で、積分できます(
とすれば、上記と全く同じ考え方で、積分できます(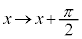 とすればよい)。
とすればよい)。
例7.  (公式です! C:積分定数)
(公式です! C:積分定数)
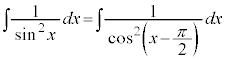
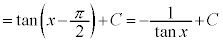 (C:積分定数)
(C:積分定数)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
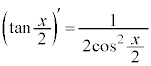 より、
より、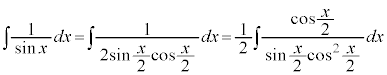
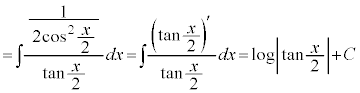 (C:積分定数)
(C:積分定数)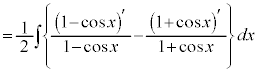
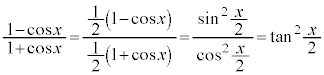 です。
です。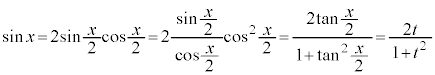 ,
,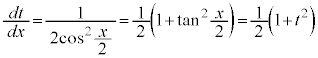 ,
,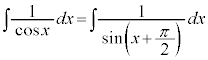 とすれば、上記と全く同じ考え方で、積分できます(
とすれば、上記と全く同じ考え方で、積分できます(