�������ȑ嗝'10�N[2]
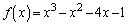 �Ƃ����B
�Ƃ����B
(1) ������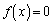 �̐��̎������ƕ��̎������͂��ꂼ�ꂢ�����邩������B
�̐��̎������ƕ��̎������͂��ꂼ�ꂢ�����邩������B (2) ������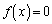 �̂��ׂĂ̎�����a�ɑ���
�̂��ׂĂ̎�����a�ɑ��� �����藧�悤�ȁA2���ȉ��̐���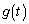 ��
��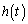 �����߂�B
�����߂�B (3) a�������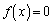 �̎������Ƃ���Ƃ��A
�̎������Ƃ���Ƃ��A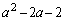 ��
��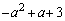 ���܂�������
���܂�������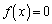 �̉��ł��邱�Ƃ������B
�̉��ł��邱�Ƃ������B (4) a�������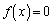 �̍ő�̎������Ƃ���Ƃ��A
�̍ő�̎������Ƃ���Ƃ��A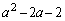 ��
��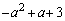 �̕����͂��ꂼ�ꐳ�A���̂ǂ���ł��邩�A���R���܂߂ē�����B
�̕����͂��ꂼ�ꐳ�A���̂ǂ���ł��邩�A���R���܂߂ē�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@3���������̖��ł����A(3)�ł́A�u�P�����v�Ɓu�����v�̈Ⴂ�ɂ��Ē��ӂ��܂��傤�B�Ȃ��A�������������Q�Ƃ��Ă��������B
(1) 3��������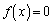 ��3�̉��������Ă��܂��Bx�ɂ��낢��Ȑ��l��������ƁA
��3�̉��������Ă��܂��Bx�ɂ��낢��Ȑ��l��������ƁA ���A������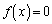 �́A
�́A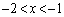 �C
�C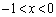 �C
�C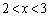 �ɂ�����1���������������܂��B�]���āA
�ɂ�����1���������������܂��B�]���āA
���̎�������1�A���̎�������2�� ......[��]
(2) 3��������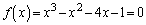 ��3�̎�������α�Cβ�Cγ�Ƃ��܂��B
��3�̎�������α�Cβ�Cγ�Ƃ��܂��B ���ꂪ���ׂĂ̎���x�ɂ��Đ��藧���߂ɁA
�@���A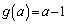 �@����C
�@����C
�ƂȂ�܂����A2���̐���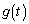 ���Ap�Cq�Cr�������Ƃ��āA
���Ap�Cq�Cr�������Ƃ��āA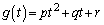 �Ƃ����ƁA�C��
�Ƃ����ƁA�C��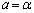 �C
�C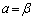 �C
�C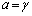 �Ƃ��āA
�Ƃ��āA �D�|�E���A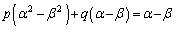 3�̉��݂͌��ɈقȂ�̂�
3�̉��݂͌��ɈقȂ�̂�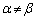 ���A
���A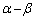 �Ŋ����āA
�Ŋ����āA 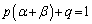 �@����G
�@����G�E�|�F���A���l�ɂ��āA
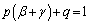 �@����H
�@����H�G�|�H���A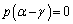
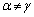 ���A
���A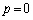 �C�G���A
�C�G���A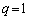 �C�D���A
�C�D���A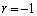
�� 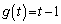 ......[��]�A���A
......[��]�A���A 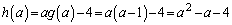 �@����I
�@����I2���̐���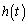 ���Al�Cm�Cn�������Ƃ��āA
���Al�Cm�Cn�������Ƃ��āA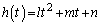 �Ƃ����ƁA�I��
�Ƃ����ƁA�I��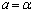 �C
�C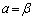 �C
�C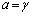 �Ƃ��āA
�Ƃ��āA �J�|�K���A
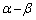 �Ŋ����āA
�Ŋ����āA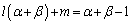 �@����M
�@����M�K�|�L���A���l�ɂ��āA
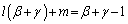 �@����N
�@����N�M�|�N���A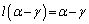
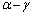 �Ŋ����āA
�Ŋ����āA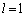
�M���A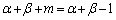
�� 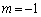 �J���A
�J���A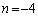
�� 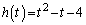
a�������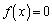 �̉��Ƃ���Ƃ��A
�̉��Ƃ���Ƃ��A 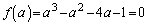
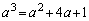 �@����O
�@����O����ꂽ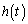 �́A�O��p���āA
�́A�O��p���āA ���A�B�����Ă��܂��B
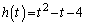 ......[��]
......[��]���ӁD�C�C�I���A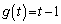 �C
�C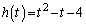 �ƂȂ邱�Ƃ͖��炩�ł����A�C�C�I��a�́u�S�Ă̎����v�ł͂Ȃ��A
�ƂȂ邱�Ƃ͖��炩�ł����A�C�C�I��a�́u�S�Ă̎����v�ł͂Ȃ��A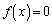 ��3��α�Cβ�Cγ�݂̂ł����āA�C�C�I��a���P�����ł͂Ȃ��A�P�����̏������g���Ȃ����Ƃɒ��ӂ��Ă��������B
��3��α�Cβ�Cγ�݂̂ł����āA�C�C�I��a���P�����ł͂Ȃ��A�P�����̏������g���Ȃ����Ƃɒ��ӂ��Ă��������B
�C�͇D�C�E�C�F���\���ď����ꂽ�����A�I�́A�J�C�K�C�L���\���ď����ꂽ�����ł����āA�ua�Ɋւ���P�����v�ł͂Ȃ��̂ł��B
��L�̂悤�ɁAp�Cq�Cr�Ɋւ���A���������D�C�E�C�F�C�܂��Al�Cm�Cn�Ɋւ���A���������J�C�K�C�L�������Ȃ��Ă��A2�����̃O���t�́A�ʉ߂���قȂ�3�_�����܂��Ă��܂��A����1�ʂ�Ɍ��܂�܂��B
�قȂ�3�_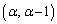 �C
�C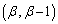 �C
�C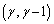 ��ʂ邱�Ƃ���
��ʂ邱�Ƃ���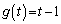 �C
�C
�قȂ�3�_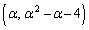 �C
�C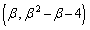 �C
�C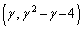 ��ʂ邱�Ƃ���
��ʂ邱�Ƃ���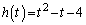
�ƒf��ł��܂��B
(3) (2)���A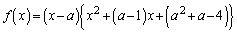
�܂��A
�����ŁA�O��p���āA
������A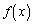 �́A
�́A �ƈ��������ł��܂��B����āA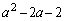 �C
�C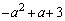 ���܂��A������
���܂��A������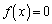 �̉��ɂȂ�܂��B
�̉��ɂȂ�܂��B
(4) (1)���A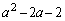 �C
�C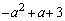 �̕����͂ǂ������ ......[��]
�̕����͂ǂ������ ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B