筑波大数学'10年[1]
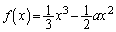とおく。ただし
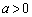とする。
(1) 
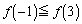となるaの範囲を求めよ。 (2) 
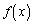の極小値が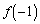
以下となるaの範囲を求めよ。 (3) 
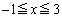における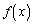
の最小値をaを用いて表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (3)では、最小値しか聞かれていませんが、最大値も考えることにします。
(1) 
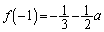
(2) 
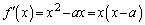(微分を参照) 
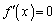とすると、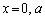
，
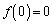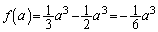
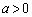より増減表は以下のようになります(3次関数の増減を参照)。増減表より、極小値は
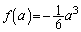です。これより、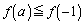
となるaの範囲は、
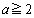......[答]
(3) まず、極小を与える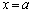
(
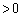)と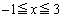
との位置関係を考えると、
，
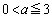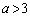の2つの場合に分けられます。 さらに、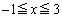
の範囲の端での関数値
，
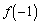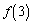と極大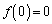値
，極小値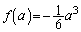
の大小関係によって場合分けすることになります。
最小値だけであれば(1)と(2)で充分ですが、最大値も考えるのであれば、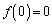
と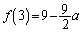
を比較します。 より、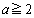
であれば
，
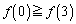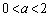であれば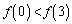
です。(1)，(2)も含めて以上より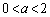、(i) 
，(ii)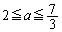 
，(iii) 
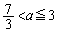，(iv)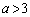 
の4つの場合に分けて考えます。
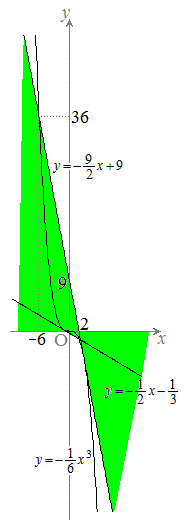(i)，(ii)，(iii)においては、
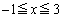の範囲内に、極大、極小を与える
，
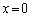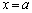いずれも含みます。(iv)においては、
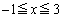の範囲内に、極大を与える
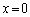は含みますが、極小を与える
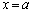は含みません。 (i)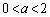 
のとき、 (ii)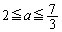 
のとき、 (iii)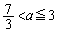 
のとき、 (iv)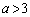 
のとき、 以上より、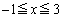
における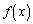
の最小値は、
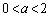のとき
，
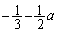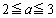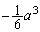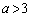のとき
，
のとき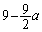
......[答] 追記．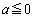
まで広げて考えると、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
と合わせて、
......[答]
，
，
より、
，
，
より、
より、
のとき、最大値：
，最小値：
のとき、最大値：
，最小値：
の範囲を動くとき、直線
の通過範囲を求めよ。」という問題になります。(i)〜(vi)により、右図黄緑色の範囲になります。本問は、このうち
の部分の下限の境界線を求めているわけです。
，
より、
