���l����H���w'10�N�O��[4]
a�Cb�𐳂̎����Ƃ���B�Ȑ�
C�F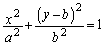
�͗̈�D�F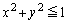 �Ɋ܂܂�Ă���B���̖₢�ɓ�����B
�Ɋ܂܂�Ă���B���̖₢�ɓ�����B
(1) 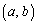 �����݂���͈͂�ab���ʏ�ɐ}������B
�����݂���͈͂�ab���ʏ�ɐ}������B (2) C���͂ޕ����̖ʐς��ő�ɂȂ�Ƃ���a�Cb�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����96�N�O��[6]�Ǝ����I�ɓ������ł��B���J�ɏꍇ�������čl���čs�����ƂɂȂ�܂��B�Ȃ��A2�����̍ő�E�ŏ��A���̑������Q�Ƃ��Ă��������B
(1) �Ȑ�C���ȉ~�ł��B�Ȑ�C��̓_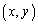 �́Aθ ��}��ϐ��Ƃ��āA
�́Aθ ��}��ϐ��Ƃ��āA �ƕ\�����Ƃ��ł��܂��B�_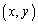 ���A�̈�D�F
���A�̈�D�F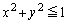 �Ɋ܂܂��Ƃ��A
�Ɋ܂܂��Ƃ��A �@��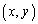 ���Ȑ�C����Ƃ��A
���Ȑ�C����Ƃ��A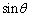 �́A
�́A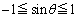 �ƂȂ邷�ׂĂ̎����l���Ƃ�܂��B
�ƂȂ邷�ׂĂ̎����l���Ƃ�܂��B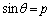 (
(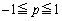 )�Ƃ����ƁA�A�́A
)�Ƃ����ƁA�A�́A 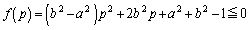 (
(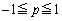 )�@����B
)�@����B(i) 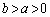 �̂Ƃ�(
�̂Ƃ�(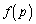 �̃O���t�͉��ɓ�)�A
�̃O���t�͉��ɓ�)�A �B �� 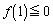 ����
���� 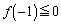
����āA
������A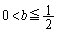 �@����C
�@����C (ii) 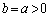 �̂Ƃ��A
�̂Ƃ��A ����āA
�� 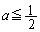 �@����D
�@����D (iii) 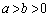 �̂Ƃ�(
�̂Ƃ�(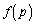 �̃O���t�͏�ɓ�)�A
�̃O���t�͏�ɓ�)�A ���̈ʒu�F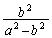 (
(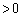 )��1��荶���E���ł���ɏꍇ�������܂��B
)��1��荶���E���ł���ɏꍇ�������܂��B ���A(a) 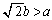 �C(b)
�C(b) 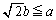 �ŏꍇ�������܂��B
�ŏꍇ�������܂��B (a) 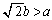 �̂Ƃ��A�܂�A
�̂Ƃ��A�܂�A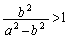 �̂Ƃ��A
�̂Ƃ��A �B �� 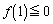
(i)�Ɠ��l�ɁA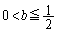 �@����E
�@����E (b) 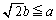 �̂Ƃ��A�܂�A
�̂Ƃ��A�܂�A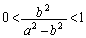 �̂Ƃ��A
�̂Ƃ��A �B �� 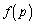 �̍ő�l�F
�̍ő�l�F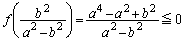
�� 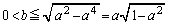 �@����F
�@����F �C�C�D�C�E�C�F���A
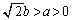 �̂Ƃ�(�C�C�D�C�E���܂Ƃ߂�)�A
�̂Ƃ�(�C�C�D�C�E���܂Ƃ߂�)�A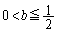 �C
�C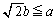 �̂Ƃ��A
�̂Ƃ��A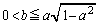
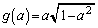 �Ƃ���ƁA
�Ƃ���ƁA 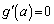 �Ƃ����
�Ƃ����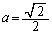 �C
�C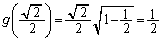
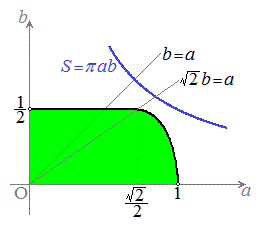 �ȏ���A
�ȏ���A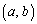 �����݂���͈͂�ab���ʏ�ɐ}������ƁA�E�}���ΐF���F��(a����Ab����������A���̋��E�����܂�)�B
�����݂���͈͂�ab���ʏ�ɐ}������ƁA�E�}���ΐF���F��(a����Ab����������A���̋��E�����܂�)�B
���������ƁA���߂�͈͂��A
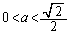 �̂Ƃ��A
�̂Ƃ��A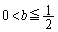 �C
�C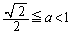 �̂Ƃ��A
�̂Ƃ��A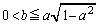
�ƌ��������邱�Ƃ��ł��܂��B
(2) �ȉ~C���͂ޖʐ�S�́A�����A�Z���̒�����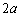 �C
�C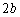 (�������́A
(�������́A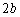 �C
�C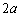 )�ƂȂ�̂ŁA
)�ƂȂ�̂ŁA 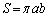 �@����G
�@����G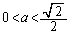 �͈̔͂�a���Œ肷��ƁAS��b���ő�l
�͈̔͂�a���Œ肷��ƁAS��b���ő�l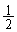 ���Ƃ�Ƃ��ɍő�l
���Ƃ�Ƃ��ɍő�l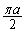 ���Ƃ�A������a�����ƁA
���Ƃ�A������a�����ƁA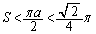
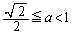 �͈̔͂�a���Œ肷��ƁAS��b���ő�l
�͈̔͂�a���Œ肷��ƁAS��b���ő�l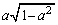 ���Ƃ�Ƃ��ɍő�l
���Ƃ�Ƃ��ɍő�l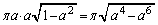 ���Ƃ�܂��B
���Ƃ�܂��B
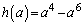 �Ƃ���ƁA
�Ƃ���ƁA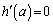 �Ƃ���ƁA
�Ƃ���ƁA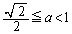 �ɂ����Ă�
�ɂ����Ă�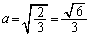 �C
�C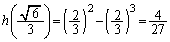 �����\���A
�����\���A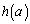 ��
��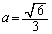 �̂Ƃ��ő�l
�̂Ƃ��ő�l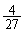 ���Ƃ�A���̂Ƃ��A
���Ƃ�A���̂Ƃ��A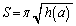 �͍ő�l
�͍ő�l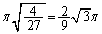 ���Ƃ�A
���Ƃ�A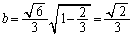 �ƂȂ�܂��B
�ƂȂ�܂��B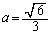 �C
�C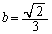 ......[��]
......[��]�ʉ��D�G�̃O���t��(1)�̐}�ɕ`�����ނƁAa���Cb�����Q�ߐ��Ƃ������p�o�Ȑ��ɂȂ�܂��B���p�o�Ȑ���S��傫������ƉE��ɂ���čs���܂��B���p�o�Ȑ��͉��ɓʂȂ̂ŁA 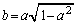 (
(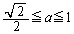 )�@����H
)�@����H�Ɛڂ���Ƃ���S�ő�ƂȂ�܂��B
�G�ƇH��A�����āA
2�悵�Đ�������ƁA
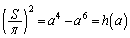 �@����I
�@����I�G�ƇH���ڂ���Ƃ��A�I���d�������̂�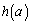 �̃O���t�̌X����0�C
�̃O���t�̌X����0�C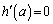 ���
���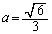
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B