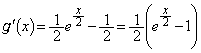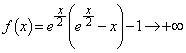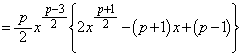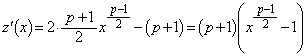�R�`��㐔�w'10�N[3]
(1) 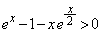 ����x�͈̔͂����߂�B
����x�͈̔͂����߂�B (3) p��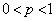 �ł���萔�Ƃ���B
�ł���萔�Ƃ���B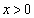 �C
�C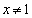 �̂Ƃ��A
�̂Ƃ��A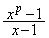 ��
��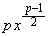 �̑召�ׂ�B
�̑召�ׂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�͊ȒP�ɒ��ׂ���@�͂Ȃ������ł��B(1)����(2)�ւ̓W�J�����p���邱�Ƃɂ��܂��B�Ȃ��A�����@�̕s�����ւ̉��p(2)���Q�Ƃ��Ă��������B
(1) 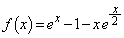 �Ƃ����܂��B
�Ƃ����܂��B 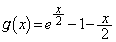 �Ƃ����܂��B
�Ƃ����܂��B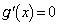 �Ƃ���ƁA
�Ƃ���ƁA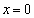
�����\���(���̑������Q��)�A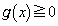
����āA�@���A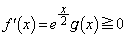 �@(������
�@(������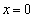 �݂̂ɂ����Đ���)�]���āA
�݂̂ɂ����Đ���)�]���āA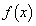 �͘A���ł����Ă���
�͘A���ł����Ă���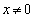 �ɂ����đ������ŁA
�ɂ����đ������ŁA
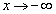 �̂Ƃ�
�̂Ƃ�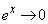 �C
�C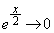 ���A
���A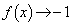
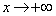 �̂Ƃ��A
�̂Ƃ��A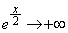 �C
�C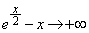 ���A
���A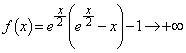
�܂��A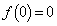
�ȏ���A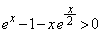 �C�܂�A
�C�܂�A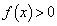 ����x�͈̔͂́A
����x�͈̔͂́A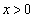 ......[��]
......[��]
(2) 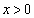 �̂Ƃ��A(1)���A
�̂Ƃ��A(1)���A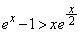
���ӂ�x�Ŋ����āA
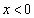 �̂Ƃ��A(1)���A
�̂Ƃ��A(1)���A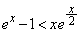
���ӂ�x�Ŋ����āA����āA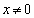 �̂Ƃ��A
�̂Ƃ��A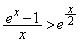
(3) (1)�C(2)���l�̃A�v���[�`�����āA�܂��A������č��ӂ���E�ӂ��������`�̊��̑����ׁA��������s���������Ƃɂ��܂��B
�����ŁA���J�b�R�����A
�Ƃ����܂��B
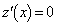 �Ƃ����ƁA
�Ƃ����ƁA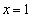
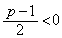 �ɒ��ӂ��đ����\�����ƁA�����\���A
�ɒ��ӂ��đ����\�����ƁA�����\���A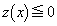 �C����āA
�C����āA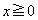 �ɂ����āA
�ɂ����āA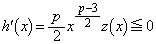 �@(������
�@(������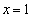 �ł̂ݐ���)
�ł̂ݐ���)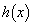 �͘A���ł����Ă���
�͘A���ł����Ă���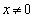 �ɂ����Č������ŁA
�ɂ����Č������ŁA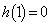 �ł��B
�ł��B
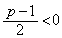 �Ȃ̂ŁA
�Ȃ̂ŁA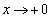 �̂Ƃ��A
�̂Ƃ��A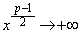 �C
�C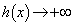 �ɒ��ӂ��āA
�ɒ��ӂ��āA
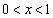 �̂Ƃ�
�̂Ƃ�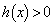 �ŁA
�ŁA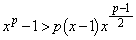 �C
�C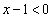 �Ŋ����āA
�Ŋ����āA����āA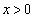 �C
�C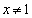 �̂Ƃ��A
�̂Ƃ��A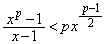 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B