�吔�w'11�N[3]
���ʏ�ɓ_O�𒆐S�Ƃ��锼�a1�̉~S��S�ɓ��ڂ��鐳�O�p�`ABC������B�ȉ��̖₢�ɓ�����B
(1) ����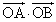 �̒l�����߂�B
�̒l�����߂�B (3) ���ʏ�̔C�ӂ̓_P�ɑ��āA�ȉ��̕s���������藧���Ƃ������B
�܂��A���������藧�̂͂ǂ̂悤�ȂƂ���������B
(4) �~S�̎���̔C�ӂ̓_Q�ɑ��āA
�ƂȂ邱�Ƃ������B
(5) �~S�̎���̔C�ӂ̓_Q�ɑ��āA
�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������p����x�N�g���̌v�Z���ł����A���̌`���悭���čH�v���Čv�Z���܂��傤�B
(1) 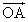 ��
��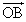 �̂Ȃ��p��
�̂Ȃ��p��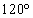 �ł��邱�ƂƁA
�ł��邱�ƂƁA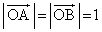 �ł��邱�ƂƂ���A
�ł��邱�ƂƂ���A 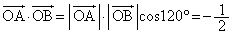 ......[��]
......[��]���l�ɁA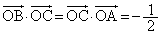
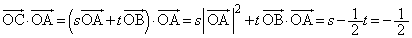 �@����@
�@����@
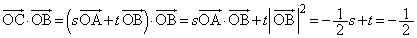 �@����A
�@����A�@�C�A��A�����ĉ����ƁA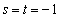
�� 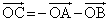 ......[��]
......[��]
��������������̂́A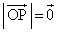 �C�܂�A�_P�����_�ɂ���Ƃ��ł��B
�C�܂�A�_P�����_�ɂ���Ƃ��ł��B
(4) p�Cq�������Ƃ��āA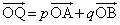 �Ƃ����܂��BQ�͉~S��̓_�Ȃ̂ŁA
�Ƃ����܂��BQ�͉~S��̓_�Ȃ̂ŁA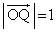 �C����āA
�C����āA 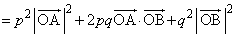
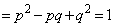 �@����B
�@����B(2)�̌��ʂ�p���āA
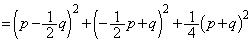
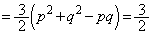 �@(�� �B)
�@(�� �B)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B