広島大理系数学'11年後期[4]
以下の問いに答えよ。
(1) 自然数a,bを11で割った余りを、それぞれr,sとする。 を11で割った余りと
を11で割った余りと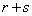 を11で割った余りは等しく、またabを11で割った余りとrsを11で割った余りは等しいことを示せ。
を11で割った余りは等しく、またabを11で割った余りとrsを11で割った余りは等しいことを示せ。 (2) a,bを自然数とする。 が11の倍数ならば、aもbも11の倍数であることを示せ。
が11の倍数ならば、aもbも11の倍数であることを示せ。 (3) 袋に1から10までの自然数を書いた玉が1個ずつ、合計10個入っている。この袋から3つの玉を同時に取り出し、書いてある数をa,b,cとする。 が11で割り切れる確率を求めよ。
が11で割り切れる確率を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 確率の問題になっていますが、実質的に剰余の問題です。なお、整数を参照してください。
(1) a,bを11で割った商をp,qとすると、余りがr,sなので、
よって、 を11で割った余りと
を11で割った余りと を11で割った余りは等しくなります。
を11で割った余りは等しくなります。 よって、abを11で割った余りとrsを11で割った余りは等しくなります。
(2) (1)より、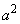 を11で割った余りと
を11で割った余りと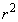 を11で割った余りは等しくなります。
を11で割った余りは等しくなります。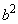 を11で割った余りと
を11で割った余りと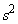 を11で割った余りは等しくなります。
を11で割った余りは等しくなります。 を11で割った余りは
を11で割った余りは を11で割った余りに等しくなります。
を11で割った余りに等しくなります。 r,sは11で割ったときの余りなので、 ,
,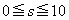 を満たします。
を満たします。
そこで、 が11で割り切れないとき、つまりrが11で割り切れず
が11で割り切れないとき、つまりrが11で割り切れず であるとき、r = 1,2,3,4,5,6,7,8,9,10について、
であるとき、r = 1,2,3,4,5,6,7,8,9,10について、 を11で割った余りを調べると、1,4,9,5,3,3,5,9,4,1となっていて、余りは1,3,4,5,9に限られています。この中から2つを選んで和を求めると、
を11で割った余りを調べると、1,4,9,5,3,3,5,9,4,1となっていて、余りは1,3,4,5,9に限られています。この中から2つを選んで和を求めると、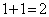 ,
, ,
,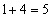 ,
,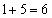 ,
,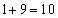 ,
,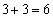 ,
,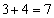 ,
,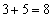 ,
,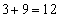 ,
,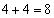 ,
, ,
,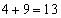 (11で割った余りは2),
(11で割った余りは2), ,
,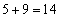 (11で割った余りは3),
(11で割った余りは3),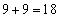 (11で割った余りは7)となり、いずれも11で割り切れません。従って、
(11で割った余りは7)となり、いずれも11で割り切れません。従って、 ,
,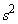 が11で割り切れない、つまり、
が11で割り切れない、つまり、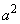 ,
, が11で割り切れないとき、
が11で割り切れないとき、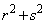 ,即ち、
,即ち、 が11で割り切れるようになる場合はありません。
が11で割り切れるようになる場合はありません。
ということは(対偶を参照)、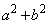 が11の倍数ならば、aもbも11の倍数であることを意味しています。
が11の倍数ならば、aもbも11の倍数であることを意味しています。
(3) 全事象は、10個の玉から3個を選ぶ選び方で、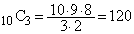 通り。
通り。 (2)で見たように、a,b,cを1から10までの自然数とするとき、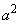 ,
, ,
,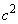 を11で割った余りは、1,3,4,5,9のどれかに限られていて、また、1,3,4,5,9の余りのどれについても、対応する自然数の書かれた玉が2個ずつ存在します。1,3,4,5,9の中から、異なる3数を選んで和を求めると、
を11で割った余りは、1,3,4,5,9のどれかに限られていて、また、1,3,4,5,9の余りのどれについても、対応する自然数の書かれた玉が2個ずつ存在します。1,3,4,5,9の中から、異なる3数を選んで和を求めると、 ,
,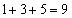 ,
, ,
,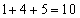 ,
,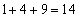 ,
, となって、
となって、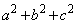 が11で割り切れる場合はありません。1を重複させて3数を選んで和を求めると、
が11で割り切れる場合はありません。1を重複させて3数を選んで和を求めると、 ,
,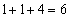 ,
, ,
,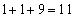 3を重複させて3数を選んで和を求めると、
3を重複させて3数を選んで和を求めると、 ,
,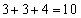 ,
, ,
,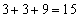 4を重複させて3数を選んで和を求めると、
4を重複させて3数を選んで和を求めると、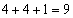 ,
,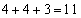 ,
,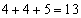 ,
,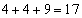 5を重複させて3数を選んで和を求めると、
5を重複させて3数を選んで和を求めると、 ,
,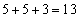 ,
, ,
,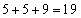 9を重複させて3数を選んで和を求めると、
9を重複させて3数を選んで和を求めると、 ,
,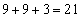 ,
,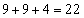 ,
,
以上の中で、11で割った余りが0になるのは、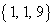 ,
,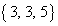 ,
, ,
, ,
,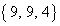 を選ぶ場合で、
を選ぶ場合で、
余りが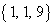 となるのは、3つの自然数a,b,cの組み合わせが、
となるのは、3つの自然数a,b,cの組み合わせが、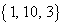 ,
,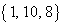 のときです。
のときです。
余りが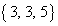 となるのは、3つの自然数a,b,cの組み合わせが、
となるのは、3つの自然数a,b,cの組み合わせが、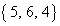 ,
,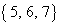 のときです。
のときです。
余りが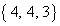 となるのは、3つの自然数a,b,cの組み合わせが、
となるのは、3つの自然数a,b,cの組み合わせが、 ,
,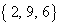 のときです。
のときです。
余りが となるのは、3つの自然数a,b,cの組み合わせが、
となるのは、3つの自然数a,b,cの組み合わせが、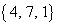 ,
,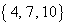 のときです。
のときです。
余りが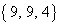 となるのは、3つの自然数a,b,cの組み合わせが、
となるのは、3つの自然数a,b,cの組み合わせが、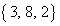 ,
,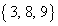 のときです。
のときです。
よって、 が11で割り切れる場合が10通りあり、求める確率は、
が11で割り切れる場合が10通りあり、求める確率は、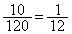 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。