���吔�w'11�N[4]
a�Cb�� ���������Ƃ��Ax��y��2��������
���������Ƃ��Ax��y��2��������
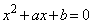 �C
�C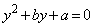
(1)  �Ƃ���Ƃ��A������������a�����ׂċ��߂�B
�Ƃ���Ƃ��A������������a�����ׂċ��߂�B (2) 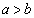 �Ƃ���Ƃ��A�������������̑g
�Ƃ���Ƃ��A�������������̑g �����ׂċ��߂�B
�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ȉ��ł́A�f�p�ɍl���Ă݂܂��B�����ł����A����ł��������ł͏[���Ɏ���I�ł��B��������A���������ɂȂ邩�ǂ������ׂ�Ƃ��A�߂��l���Ƃ镽���� ��T���Ă��āA
��T���Ă��āA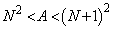 �Ƃ����`�̕s��������邱�Ƃ��ł���AA�͕������ł͂Ȃ��A�ƁA�f��ł��܂��B(2)�͂�����g���ĉ��܂��B
�Ƃ����`�̕s��������邱�Ƃ��ł���AA�͕������ł͂Ȃ��A�ƁA�f��ł��܂��B(2)�͂�����g���ĉ��܂��B
 �@����@
�@����@�ƂȂ�܂��By��2��������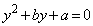 �����`�̕������ł��B���̉��́A
�����`�̕������ł��B���̉��́A ���ꂪ�����ƂȂ邽�߂ɁA���Ȃ��Ƃ��A������ ��0�܂��͕������ł���K�v������܂��B
��0�܂��͕������ł���K�v������܂��B (i) 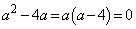
�Ƃ���ƁA ���A
���A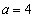
���̂Ƃ��A �Ŋm���ɇ@�͐������������܂��B
�Ŋm���ɇ@�͐������������܂��B (ii) p�����R���Ƃ��āA
�Ƃ������Ƃ��܂��B�����a�ɂ��ĉ����ƁA
a�͐����Ȃ̂ŁA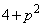 (
(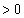 )�͕������ł��Bq�����R���Ƃ��āA
)�͕������ł��Bq�����R���Ƃ��āA �Ƃ����܂��B
������A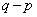 �C
�C �͂������4�̖ł��B
�͂������4�̖ł��B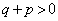 �C
�C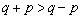 �Ȃ̂ŁA
�Ȃ̂ŁA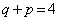 �C
�C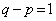 �Ɍ����܂����A
�Ɍ����܂����A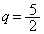 �C
�C �ƂȂ�Ap�Cq�͎��R���ł͂���܂���B�]���āA���̏ꍇ�ɁA
�ƂȂ�Ap�Cq�͎��R���ł͂���܂���B�]���āA���̏ꍇ�ɁA ���������ƂȂ邱�Ƃ͂���܂���B
���������ƂȂ邱�Ƃ͂���܂���B �ȏ���A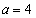 ......[��]
......[��]
(2) x��2��������
 �@����A
�@����A�̉��́A
 �@����B
�@����By��2��������
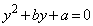 �@����C
�@����C�̉��́A
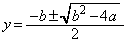 �@����D
�@����D�A�C�C���������������߂ɁA�B�C�D�̍�����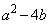 �C
�C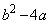 ��0�܂��͕������ł���K�v������܂��B
��0�܂��͕������ł���K�v������܂��B (i) 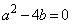
�Ƃ���ƁA �C
�C ���A
���A ����āA �Ɍ����܂����A
�Ɍ����܂����A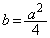 �������ɂȂ�̂́A
�������ɂȂ�̂́A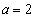 �C
�C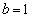 �̂Ƃ��ŁA���̂Ƃ��A
�̂Ƃ��ŁA���̂Ƃ��A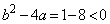
����āA���̏ꍇ�ɂ́A�����ɓK����a�Cb�̑g�͂���܂���B (ii) 
�Ƃ���ƁA �C
�C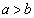 ���A
���A �܂��A �͐����Ȃ̂ŁAb�͋�����k�����R���Ƃ���
�͐����Ȃ̂ŁAb�͋�����k�����R���Ƃ���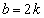 �Ƃ����ƁA
�Ƃ����ƁA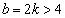 ���A
���A �C�܂��A
�C�܂��A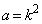 (i)�̏ꍇ���s�K�������̂ŁA
(i)�̏ꍇ���s�K�������̂ŁA (
(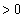 )�͕������ł����A
)�͕������ł����A �����ŁA �ł��B
�ł��B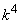 �̎��ɏ����ȕ�������
�̎��ɏ����ȕ�������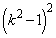 �ł��B
�ł��B �Ƃ����ƁA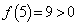 ���A
���A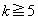 �ł���A
�ł���A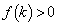 �C���Ȃ킿�A
�C���Ȃ킿�A �ƂȂ�A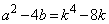 �͕������ɂȂ蓾�܂���B
�͕������ɂȂ蓾�܂���B
���́A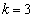 �̂Ƃ���
�̂Ƃ���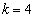 �̂Ƃ��ł����A
�̂Ƃ��ł����A �͂Ƃ��ɕ������ł͂���܂���B
����āA(ii)�̏ꍇ�ɂ��A�����ɓK����a�Cb�̑g�͂���܂���B
(iii) 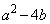 �C
�C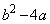 ���Ƃ��ɕ������ƂȂ�ꍇ�A
���Ƃ��ɕ������ƂȂ�ꍇ�A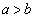 ���Ak�����R���Ƃ��āA
���Ak�����R���Ƃ��āA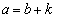 �Ƃ����ƁA
�Ƃ����ƁA 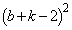 �̎��ɑ傫�ȕ�������
�̎��ɑ傫�ȕ������� �ł��B
�ł��B���ꂪ0�ɓ������Ƃ��A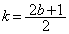 �ƂȂ�܂����Ak�͐����Ȃ̂ŁA
�ƂȂ�܂����Ak�͐����Ȃ̂ŁA �ƂȂ邱�Ƃ͂���܂���B���ɑ傫�ȕ�������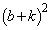 �ł����A
�ł����A ����āA
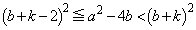 ����
���� 
�]���āA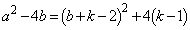 �́A
�́A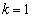 �̂Ƃ��ɂ̂݁A������
�̂Ƃ��ɂ̂݁A������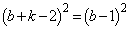 �ɂȂ�܂��B���̂Ƃ��A
�ɂȂ�܂��B���̂Ƃ��A  �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA�ƂȂ�A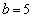 �̂Ƃ�������1�ɂȂ邱�Ƃ��킩��܂��B
�̂Ƃ�������1�ɂȂ邱�Ƃ��킩��܂��B �Ȃ̂ŁA �̎��ɏ����ȕ�����
�̎��ɏ����ȕ����� ��
��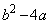 �Ƃ��ׂĂ݂܂��B
�Ƃ��ׂĂ݂܂��B 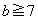 �ł́A
�ł́A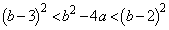 �ƂȂ�A
�ƂȂ�A ���������ɂȂ邱�Ƃ͂���܂���B
���������ɂȂ邱�Ƃ͂���܂���B
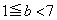 �̂Ƃ��́A
�̂Ƃ��́A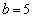 �̂Ƃ��̂�
�̂Ƃ��̂�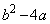 ��������1�ƂȂ�A���̂Ƃ��A
��������1�ƂȂ�A���̂Ƃ��A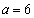 �ł��B
�ł��B
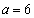 �C
�C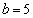 �̂Ƃ��A2���������A�́A
�̂Ƃ��A2���������A�́A���A������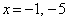 �������܂��B2���������C�́A
�������܂��B2���������C�́A ���A������ �C
�C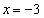 �������܂��B
�������܂��B �ȏ���A �C
�C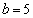 ......[��]
......[��]
�ʉ��D�ŏ�����������̉����ǂ̂悤�ɂȂ邩���ׂĂ����A�ȉ��̂悤�ɂ��āA�ȒP�ɉ������Ƃ��ł��܂��B
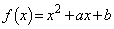 �C
�C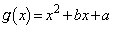
�Ƃ����ƁA��2���������́A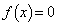 �C
�C �ƂȂ�܂��B
�ƂȂ�܂��B 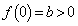 �C
�C �C
�C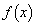 �̎��ʒu�G
�̎��ʒu�G �C
�C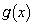 �̎��ʒu�F
�̎��ʒu�F �@����E
�@����E���A��2���������������������ĂA�Ƃ��ɕ��̐������ł��B
(1) 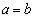 �̂Ƃ��A��2���������͂Ƃ��ɁA
�̂Ƃ��A��2���������͂Ƃ��ɁA �ƂȂ�܂��B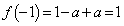 ���
���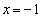 �͉��ɂȂ�Ȃ��̂ŁA
�͉��ɂȂ�Ȃ��̂ŁA a�͐����Ȃ̂ŁA ��1�̖ł��邱�Ƃ�
��1�̖ł��邱�Ƃ�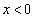 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A ���A��������
���A��������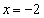 �Ɍ����܂��B����āA
�Ɍ����܂��B����āA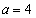 ......[��]
......[��] (2) 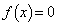 �C
�C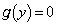 �̉������̐����ł��邱�Ƃ���A�E���A
�̉������̐����ł��邱�Ƃ���A�E���A  �C
�C
�܂�A
 �C
�C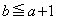
�́A������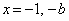 �������܂��B
�������܂��B 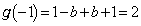 ���
���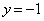 �͉��ɂȂ�Ȃ��̂ŁA
�͉��ɂȂ�Ȃ��̂ŁAb�͐����Ȃ̂ŁA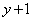 ��2�̖ł��邱�Ƃ�
��2�̖ł��邱�Ƃ�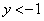 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A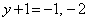 �Ɍ����܂��B������ɂ��Ă��A
�Ɍ����܂��B������ɂ��Ă��A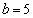 �C
�C ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B