大阪市大数学'11年[3]
p,qは正の実数で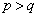 とする。
とする。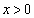 において、2つの関数
において、2つの関数
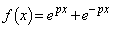 ,
,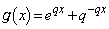
問1 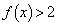 を示せ。
を示せ。 問2 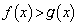 を示せ。
を示せ。 問3 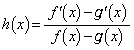 とするとき、
とするとき、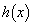 は
は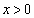 において単調減少であることを示せ。
において単調減少であることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 問3が苦労させられます。
等号成立は、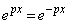 ,つまり、
,つまり、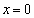 のときですが、
のときですが、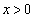 においては、等号は成立せず、
においては、等号は成立せず、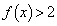
∴ 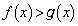
問3 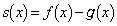 とおくと、
とおくと、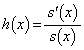 です。
です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 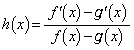 とするとき、
とするとき、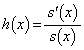 です。
です。