�啪��㐔�w'11�N[1]
���� �C
�C �C
�C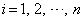 �ɑ��Ď��̕s�������ؖ�����B�������An�͎��R���ł���B
�ɑ��Ď��̕s�������ؖ�����B�������An�͎��R���ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�R�[�V�[�E�V�������c�̕s��������ʓI�ȏꍇ�ŏؖ�������ł��B�������ň��S�m���ɓ��Ă������Ȃ�ȉ��̂悤�����w�I�A�[�@�ŏؖ�����̂ł��傤���A�����ƃ��N�ɏؖ�������@������܂��B
(�T)  �̂Ƃ��A
�̂Ƃ��A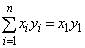
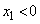 ����
���� 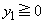 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A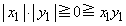
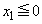 ����
���� 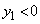 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A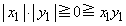
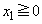 ����
���� 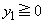 �̏ꍇ�A�܂��́A
�̏ꍇ�A�܂��́A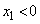 ����
����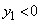 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A
����Ă��ׂĂ̏ꍇ�ɂ����āA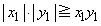
�^���͐������܂��B(�U) 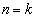 �̂Ƃ��A
�̂Ƃ��A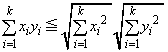 ����������Ɖ��肵�܂��B
����������Ɖ��肵�܂��B ���ӂ�2�悵���s�����̗��ӂɁA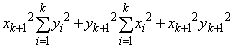 ��������ƁA
��������ƁA ����āA
����āA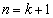 �̂Ƃ��ɂ��A�^�s�����͐������܂��B
�̂Ƃ��ɂ��A�^�s�����͐������܂��B (�T)�C(�U)���A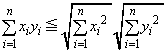 ���������܂��B
���������܂��B
�NjL�D�R�[�V�[�E�V�������c�̕s�����𗘗p������́A�Ⴆ�A���H��'08�N�O��[3]�̂悤�Ȗ�肪����܂��B���̉ł������܂������A�{��ł͈ȉ��̂悤�ȉ��\�ł��B ���������܂��B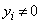 (
(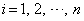 )�ł���A�����́A
)�ł���A�����́A �ƂȂ�Ƃ��ɐ������܂��B
�ƂȂ�Ƃ��ɐ������܂��B
���ӂ�ό`���āA ������At ��2���������F
�́A�d���������A�������������A���ʎ�D�ɂ��āA
 ���A
���A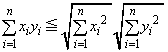
�ϕ��`���̃R�[�V�[��V�������c�̕s�����F�ł��A���l�̏ؖ����\�ł��B�C�ӂ̊� �C
�C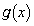 �ɂ��āA
�ɂ��āA �ƂȂ�܂����A���ӂ�ό`���āA
������At ��2���������F
�́A�d���������A�������������A���ʎ�D�ɂ��āA
��  �{���
�{���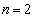 �̏ꍇ�ɂ́A���ό`�����ŏؖ��ł��܂��B
�̏ꍇ�ɂ́A���ό`�����ŏؖ��ł��܂��B �E�ӂ��獶�ӂ������āA
�� 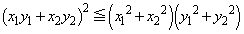 �ȉ���
�ȉ���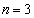 �̏ꍇ�ɂ́A���ς��g���ĊȒP�ɏؖ����邱�Ƃ��ł��܂��B
�̏ꍇ�ɂ́A���ς��g���ĊȒP�ɏؖ����邱�Ƃ��ł��܂��B
���������'11�N[1]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
a�Cb�Cc�Cx�Cy�Cz�������Ƃ���B (�A) 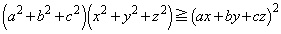
(�C)  �̂Ƃ��A
�̂Ƃ��A �̍ŏ��l�����߂�B
�̍ŏ��l�����߂�B 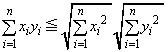
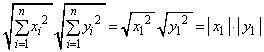
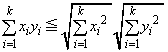 ����������Ɖ��肵�܂��B
����������Ɖ��肵�܂��B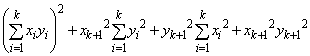


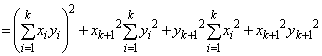
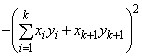

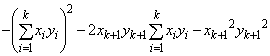
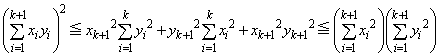
 ���A
���A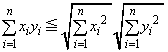
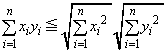 ���������܂��B
���������܂��B
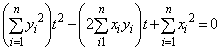
 ���A
���A