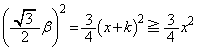��嗝�n���w'11�N�O��[4]
a�Cb�Cc�𐳂̒萔�Ƃ��Ax�̊�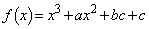 ���l����B�ȉ��A�萔�͂��ׂĎ����Ƃ���B
���l����B�ȉ��A�萔�͂��ׂĎ����Ƃ���B
(1) �萔p�Cq�ɑ��A�����݂����萔r�����݂��邱�Ƃ������B
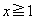 �Ȃ��
�Ȃ�� 
(2) �P���� ��p���āA�����݂����萔k�Cl�����݂��邱�Ƃ������B
��p���āA�����݂����萔k�Cl�����݂��邱�Ƃ������B  �Ȃ��
�Ȃ�� 
(3) ���ׂĂ̎��R��n�ɑ��āA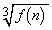 �����R���ł���Ƃ���B���̂Ƃ���
�����R���ł���Ƃ���B���̂Ƃ���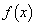 �́A���R���̒萔m��p����
�́A���R���̒萔m��p���� �ƕ\����邱�Ƃ������B
�ƕ\����邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������Ƃ��Ă͂��܂茩�����Ȃ��^�C�v�̖��ł��B�u�萔�����݂��邱�Ƃ������v�Ƃ������ɑ��ẮA�萔�����߂�菇���������A���݂��邱�Ƃ����������ƂɂȂ�܂��B�Ȃ��A�����A�����Ɩ������Q�Ƃ��Ă��������B
(1) �O�p�s�����F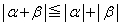 �ɂ����āAα��px�Cβ ��q�Ƃ���ƁA
�ɂ����āAα��px�Cβ ��q�Ƃ���ƁA �ɂ����ẮA
�ɂ����ẮA �����ŁA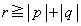 ���݂����悤�Ȓ萔r���Ƃ�ƁA
���݂����悤�Ȓ萔r���Ƃ�ƁA �ɂ����āA
�ɂ����āA �Ƃł��܂��B����āA �Ȃ�A
�Ȃ�A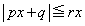 ���݂����萔r�����݂��܂��B
���݂����萔r�����݂��܂��B
(2) ��ӂ��݂���k�����݂���Ƃ��āA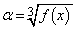 �C
�C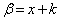 �Ƃ���ƁA
�Ƃ���ƁA �ł����A�����ŁAk�����̒萔�ł���A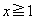 �ɂ����āA
�ɂ����āA 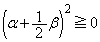 �Ȃ̂ŁA
�Ȃ̂ŁA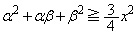 �C
�C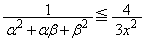 �@����@
�@����@�܂��A
�����ŁA���̒萔k��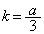 �ł���A
�ł���A (1)�̌��ʂɂ����āA �C
�C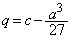 �Ƃ���A
�Ƃ���A 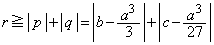 �@����A
�@����A�����悤�Ȓ萔r���Ƃ�A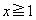 �ɂ����āA
�ɂ����āA 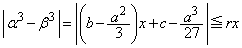 �@����B
�@����B�@�C�B���A
�����A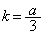 �Ƃ��A�A���݂����悤�Ȓ萔r���Ƃ�A
�Ƃ��A�A���݂����悤�Ȓ萔r���Ƃ�A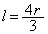 �ƂȂ�悤�ɒ萔k�Cl���Ƃ�A
�ƂȂ�悤�ɒ萔k�Cl���Ƃ�A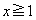 �ɂ����āA
�ɂ����āA �Ƃ��邱�Ƃ��ł��܂��B����āA��ӂ��݂����萔k�Cl�����݂��܂��B
(3) (2)�̌��ʂɂ����āA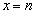 (n�͔C�ӂ̎��R��)�Ƃ���ƁA
(n�͔C�ӂ̎��R��)�Ƃ���ƁA 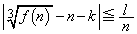 ��
��  �@����C
�@����C�����ŁAa�Cb�Cc�����ł��邱�Ƃ���A
�܂�A �Ȃ̂ŁA
�Ȃ̂ŁA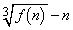 �͎��R���ł��Bn���\���ɑ傫���Ƃ�A�C�͈̔́F
�͎��R���ł��Bn���\���ɑ傫���Ƃ�A�C�͈̔́F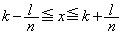 �ɓ��鎩�R��x������1�ɂł��܂��B���̎��R����m�Ƃ���ƁA
�ɓ��鎩�R��x������1�ɂł��܂��B���̎��R����m�Ƃ���ƁA  �@(���̂Ƃ��A
�@(���̂Ƃ��A �A�܂�A
�A�܂�A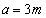 �Ɍ����܂�)
�Ɍ����܂�)���̂Ƃ��A
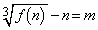 �C
�C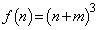
�ƂȂ�A
�ƕ\����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B