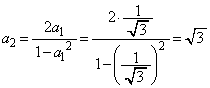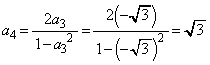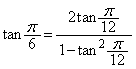九大数学'11年前期[3]
数列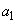 ,
,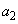 ,・・・,
,・・・, ,・・・ は
,・・・ は
 ,
, 
(1) 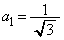 とするとき、一般項
とするとき、一般項 を求めよ。
を求めよ。 (2) 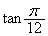 の値を求めよ。
の値を求めよ。 (3) 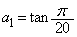 とするとき、
とするとき、  ,
, 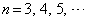
をみたす最小の自然数kを求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 与えられた漸化式の意味するところに気づければ容易です。
(1) まず、与えられた漸化式で、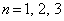 として感触をつかみます。
として感触をつかみます。 以後、 と
と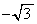 の繰り返しになります。偶数番目の項が
の繰り返しになります。偶数番目の項が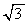 ,奇数番目の項が
,奇数番目の項が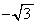 です。
です。
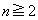 のとき、
のとき、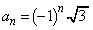 ,但し、
,但し、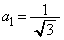 ......[答]問題文に「一般項」とあるので、統一的に一つの式で記述したければ、
......[答]問題文に「一般項」とあるので、統一的に一つの式で記述したければ、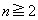 のときに1,
のときに1,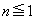 のときに
のときに となるようなものを探します。例えば、
となるようなものを探します。例えば、 です。これを使えば、
です。これを使えば、  (
( )
)と記述できます。実は、(2)以下から、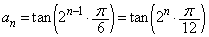 となることがわかります。
となることがわかります。
 より、
より、 より、
より、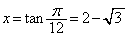 ......[答]
......[答]
(1),(2)の結果より、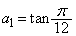 とすると、
とすると、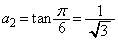 ,
, ,
,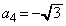 ,
,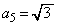 ,・・・ となって、
,・・・ となって、 では、
では、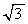 と
と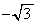 が繰り返し、数列
が繰り返し、数列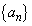 が周期を持つことがわかります。
が周期を持つことがわかります。
(3) (2)をヒントとして、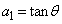 とすると、
とすると、 となり、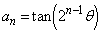 となっていることがわかります。
となっていることがわかります。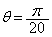 のときには、
のときには、 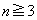 のとき、
のとき、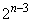 と5は互いに素なので、mは
と5は互いに素なので、mは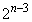 の倍数で、jを整数として、
の倍数で、jを整数として、 とおけます。
とおけます。 としていくと、
としていくと、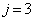 のときに、
のときに、 ,
,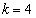 となり、
となり、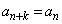 となります。よって、
となります。よって、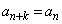 ,
,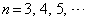 を満たす最小の自然数kは、
を満たす最小の自然数kは、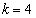 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。