島根大医数学'11年[1]
mを自然数とする。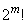 が
が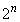 で割り切れる自然数nの最大値を
で割り切れる自然数nの最大値を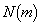 とおくとき、次の問いに答えよ。
とおくとき、次の問いに答えよ。
(1) 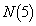 を求めよ。
を求めよ。 (2) 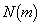 をmの式で表せ。
をmの式で表せ。 (3) 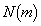 が素数ならば、mも素数であることを証明せよ。
が素数ならば、mも素数であることを証明せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 類題が東工大'07前期[1],東工大'91年前期[1]にあります。なお、整数を参照してください。
(1) 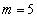 のとき、
のとき、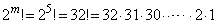
1から32までの整数の中に2の倍数は16個あります。
この16個のうち、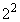 の倍数が8個(4,8,12,16,20,24,28,32)あります。
の倍数が8個(4,8,12,16,20,24,28,32)あります。
この8個のうち、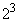 の倍数が4個(8,16,24,32)あります。
の倍数が4個(8,16,24,32)あります。
この4個のうち、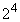 の倍数が2個(16,32)あります。
の倍数が2個(16,32)あります。
この2個のうち、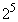 の倍数が1個(32)あります。
の倍数が1個(32)あります。
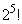 を素因数分解すると、2の個数は、
を素因数分解すると、2の個数は、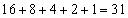
∴ 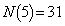 ......[答]
......[答]
(2) 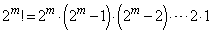
1から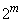 までの整数の中に2の倍数は
までの整数の中に2の倍数は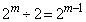 個あります。
個あります。
この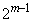 個のうち、
個のうち、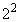 の倍数は
の倍数は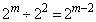 個あります。
個あります。
同様に、1から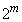 までの整数の中に
までの整数の中に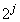 (
(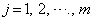 )の倍数は、
)の倍数は、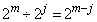 個あります。(1)と同様に考えて、
個あります。(1)と同様に考えて、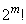 を素因数分解すると、2の個数は、
を素因数分解すると、2の個数は、 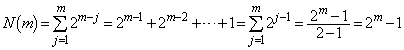 ......[答]
......[答]
(3) 元の命題の対偶「mが素数でなければ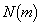 は素数でない」を証明します。
は素数でない」を証明します。 mが素数でなければ、2以上の整数a,bで、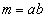 となるものが存在します。
となるものが存在します。
このとき、(2)の結果を用いて、 ここで、
より、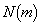 は素数ではありません。(証明終)
は素数ではありません。(証明終)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 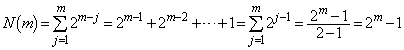 ......[答]
......[答]