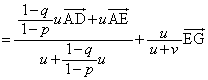�M�B��㐔�w'11�N[2]
���_�𒆐S�Ƃ��锼�a1�̉~S�Ɠ_A ���l����B�������A
���l����B�������A �C
�C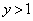 �Ƃ���B�_A�Ɠ_B
�Ƃ���B�_A�Ɠ_B �����Ԓ����Ɖ~S�Ƃ̌�_��D�C�_A��C
�����Ԓ����Ɖ~S�Ƃ̌�_��D�C�_A��C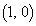 �����Ԓ����Ɖ~S�Ƃ̌�_��E�Ƃ���B�_D����ѓ_E����x���ɉ��낵�������̑������ꂼ��F�����G�Ƃ���B����DG�ƒ���EF�̌�_��M�Ƃ���Ƃ�����AM��x���ɒ������邱�Ƃ������B
�����Ԓ����Ɖ~S�Ƃ̌�_��E�Ƃ���B�_D����ѓ_E����x���ɉ��낵�������̑������ꂼ��F�����G�Ƃ���B����DG�ƒ���EF�̌�_��M�Ƃ���Ƃ�����AM��x���ɒ������邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�}�`�ƕ������A���ʃx�N�g���A2�ʂ�̉�@�ōl���Ă݂܂��B�ǂ���ɂ��Ă��v�Z�͂��Ȃ�ʓ|�ł��B
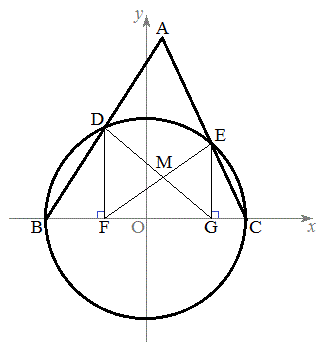
��@1
�_D��x���W��b (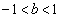 )�Ƃ���ƁAy���W��
)�Ƃ���ƁAy���W�� �ł��B
�ł��B
����BD�̕������́A2�_B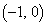 �CD
�CD ��ʂ邱�Ƃ���(�����̕��������Q��)�A
��ʂ邱�Ƃ���(�����̕��������Q��)�A  �@����@
�@����@�_E��x���W��c (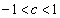 )�Ƃ���ƁAy���W��
)�Ƃ���ƁAy���W�� �ł��B
�ł��B
����CE�̕������́A2�_C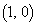 �CE
�CE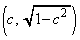 ��ʂ邱�Ƃ���A
��ʂ邱�Ƃ���A  �@����A
�@����A����DG�̕������́A2�_D�CG ��ʂ钼���Ƃ��āA
��ʂ钼���Ƃ��āA  �@����B
�@����B����EF�̕������́A2�_E�CF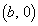 ��ʂ钼���Ƃ��āA
��ʂ钼���Ƃ��āA 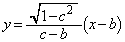 �@����C
�@����C�@�C�A��A�����A��_A��x���W�́A
�� 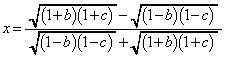 �@����D
�@����D
�B�C�C��A�����A��_M��x���W�́A �� 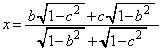 �@����E
�@����E
�D�ɂ��āA�E�ӂ��L��������ƁA �E�ɂ��āA�E�ӂ�L��������ƁA
����āA�_A�Ɠ_M��x���W�͈�v���A����AM��x���ɐ����ł��B
��@2
A����BC�ɉ��낵�������̑���H�Ƃ��܂��B
�Ƃ��܂��B�܂��A �C
�C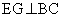 ���A
���A �C
�C �Ƃ��܂��B
�Ƃ��܂��B
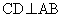 �C
�C �ɒ��ӂ��܂��B
�ɒ��ӂ��܂��B
��ABH �� ��CBD���ABH�FAB �� BD�FBC�� 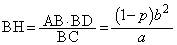 ��ACH �� ��BCE���ACH�FAC �� CE�FBC��
��ACH �� ��BCE���ACH�FAC �� CE�FBC�� 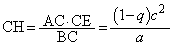 ����āABH�FCH ��
����āABH�FCH �� 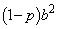 �F
�F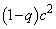
��ACD �� ��BAE���AAD�FAC �� AE�FAB
pb�Fc ��qc�Fb
�� 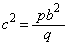
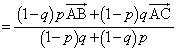 �@����F
�@����F��BDF �� ��BAH���ADF�FAH �� BD�FAB
u�F1 �� 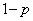 �F1
�F1 �� 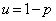 ��CEG �� ��CAH���AEG�FAH �� CE�FCA
��CEG �� ��CAH���AEG�FAH �� CE�FCA v�F1 ��  �F1
�F1 �� 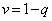 ��
�� 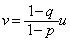
DM�FMG �� DF�FEG �� u�Fv�ƁA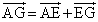 ���A
���A ����āA �ł��B
�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 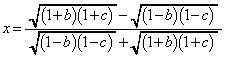 �@����D
�@����D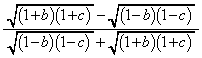



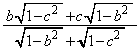
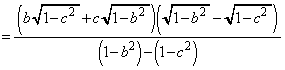
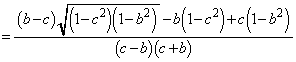
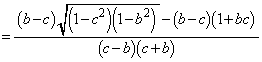
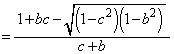

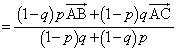 �@����F
�@����F