���k�嗝�n���w'11�N�O��[1]
����a�ɑ��A�s����
�̕\�����W���ʏ�̗̈��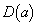 �Ƃ����B
�Ƃ����B
(1) 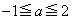 �������ׂĂ�a�ɑ�
�������ׂĂ�a�ɑ�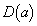 �̓_�ƂȂ�悤�ȓ_
�̓_�ƂȂ�悤�ȓ_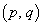 �͈̔͂�}������B
�͈̔͂�}������B (2) 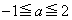 ���������ꂩ��a�ɑ�
���������ꂩ��a�ɑ�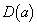 �̓_�ƂȂ�悤�ȓ_
�̓_�ƂȂ�悤�ȓ_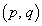 �͈̔͂�}������B
�͈̔͂�}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶���́u���ׂẮv�A�u�����ꂩ�́v�Ƃ������t���ǂ������������ł��B
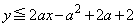 �@����@
�@����@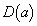 �́A����
�́A����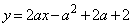 ���牺�����̈��ł��B�����ł́Ax�Cy���Œ肵�A�@��ό`���āA
���牺�����̈��ł��B�����ł́Ax�Cy���Œ肵�A�@��ό`���āA
�Ƃ��āA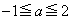 �ɂ�����a��2����
�ɂ�����a��2����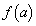 ���l���܂��B
���l���܂��B
�@ �� 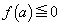
�ł��B
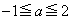 �������ׂĂ�a�ɑ�
�������ׂĂ�a�ɑ�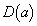 �̓_�ƂȂ�A�Ƃ������Ƃ́A
�̓_�ƂȂ�A�Ƃ������Ƃ́A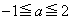 �ɂ����Ă˂�
�ɂ����Ă˂�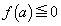 �C�܂�A
�C�܂�A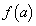 �̍ő�l��0�ȉ��ɂȂ�Ƃ������Ƃł��B
�̍ő�l��0�ȉ��ɂȂ�Ƃ������Ƃł��B
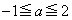 ���������ꂩ��a�ɑ�
���������ꂩ��a�ɑ�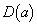 �̓_�ƂȂ�A�Ƃ������Ƃ́A
�̓_�ƂȂ�A�Ƃ������Ƃ́A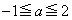 �ɂ�����
�ɂ�����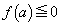 �ƂȂ�a�����Ȃ��Ƃ�1����A�܂�A
�ƂȂ�a�����Ȃ��Ƃ�1����A�܂�A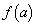 �̍ŏ��l��0�ȉ��ɂȂ�Ƃ������Ƃł��B
�̍ŏ��l��0�ȉ��ɂȂ�Ƃ������Ƃł��B
�]���āA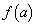 ��
��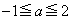 �ɂ������ő�l�ƍŏ��l���l����悢�킯�ł��B
�ɂ������ő�l�ƍŏ��l���l����悢�킯�ł��B
(i) 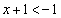 �C�܂�A
�C�܂�A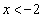 �̂Ƃ��A
�̂Ƃ��A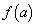 ��
��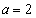 �̂Ƃ��ɍő�l�F
�̂Ƃ��ɍő�l�F ���Ƃ�܂��B�܂��A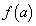 ��
��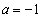 �̂Ƃ��ɍŏ��l�F
�̂Ƃ��ɍŏ��l�F
���Ƃ�܂��B
(ii) 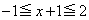 �C�܂�A
�C�܂�A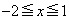 �̂Ƃ��A
�̂Ƃ��A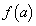 ��
��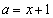 �̂Ƃ��ɍŏ��l�F
�̂Ƃ��ɍŏ��l�F 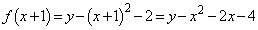 ���Ƃ�܂��B
���Ƃ�܂��B���ʒu�F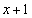 ���͈͂̒��ԓ_
���͈͂̒��ԓ_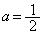 ���獶���ɂ���Ƃ��A�܂�A
���獶���ɂ���Ƃ��A�܂�A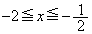 �̂Ƃ��A
�̂Ƃ��A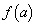 �͔͈͂̉E�[
�͔͈͂̉E�[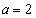 �ɂ����āA�ő�l�F
�ɂ����āA�ő�l�F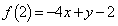 ���Ƃ�܂��B
���Ƃ�܂��B ���ʒu�F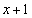 ���͈͂̒��ԓ_
���͈͂̒��ԓ_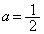 ����E���ɂ���Ƃ��A�܂�A
����E���ɂ���Ƃ��A�܂�A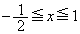 �̂Ƃ��A
�̂Ƃ��A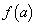 �͔͈͂̍��[
�͔͈͂̍��[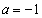 �ɂ����āA�ő�l�F
�ɂ����āA�ő�l�F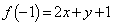 ���Ƃ�܂��B
���Ƃ�܂��B (iii) 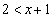 �C�܂�A
�C�܂�A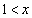 �̂Ƃ��A
�̂Ƃ��A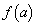 ��
��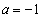 �̂Ƃ��ɍő�l�F
�̂Ƃ��ɍő�l�F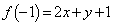 ���Ƃ�܂��B�܂��A
���Ƃ�܂��B�܂��A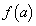 ��
��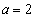 �̂Ƃ��ɍŏ��l�F
�̂Ƃ��ɍŏ��l�F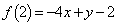 ���Ƃ�܂��B
���Ƃ�܂��B
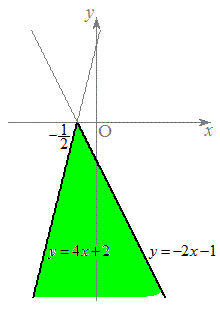 (1)
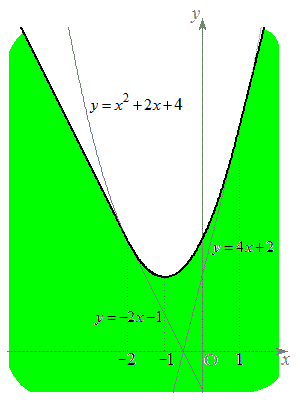
(1) 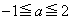 �������ׂĂ�a�ɑ�
�������ׂĂ�a�ɑ�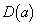 �̓_�ƂȂ�悤�ȓ_
�̓_�ƂȂ�悤�ȓ_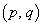 �͈̔͂́A
�͈̔͂́A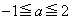 �ɂ�����
�ɂ�����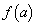 �̍ő�l��0�ȉ��ɂȂ邱�Ƃ���A
�̍ő�l��0�ȉ��ɂȂ邱�Ƃ���A�}������ƉE�}���ΐF���F��(�������E�����܂�)�B
 (2)
(2) 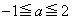 ���������ꂩ��a�ɑ�
���������ꂩ��a�ɑ�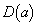 �̓_�ƂȂ�悤�ȓ_
�̓_�ƂȂ�悤�ȓ_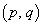 �͈̔͂́A
�͈̔͂́A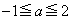 �ɂ�����
�ɂ�����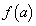 �̍ŏ��l��0�ȉ��ɂȂ邱�Ƃ���A
�̍ŏ��l��0�ȉ��ɂȂ邱�Ƃ���A�E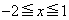 �̂Ƃ��A
�̂Ƃ��A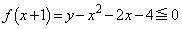
�� 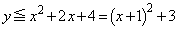
�}������ƉE�}���ΐF���F��(�������E�����܂�)�B
(1)�̕ʉ��D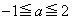 �������ׂĂ�a�ɑ���
�������ׂĂ�a�ɑ���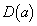 �̓_�ƂȂ�_
�̓_�ƂȂ�_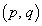 �͈̔͂�E�Ƃ��܂��B
�͈̔͂�E�Ƃ��܂��B 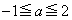 �������ׂĂ�a�ɑ���
�������ׂĂ�a�ɑ���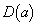 �̓_�ƂȂ�A�Ƃ������Ƃ́A
�̓_�ƂȂ�A�Ƃ������Ƃ́A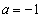 �̂Ƃ���
�̂Ƃ���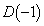 ��E���܂ށA�Ƃ������Ƃł��B�܂��A
��E���܂ށA�Ƃ������Ƃł��B�܂��A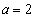 �̂Ƃ���
�̂Ƃ���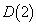 ��E���܂ށA�Ƃ������Ƃł��B�]���āA
��E���܂ށA�Ƃ������Ƃł��B�]���āA�ł��B�@�́A
�E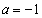 �̂Ƃ��A
�̂Ƃ��A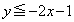
�E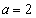 �̂Ƃ��A
�̂Ƃ��A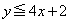
�ƂȂ�̂ŁA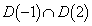 �́A����
�́A����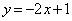 ���牺���ł�����
���牺���ł�����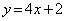 ���牺���̗̈�ł��B
���牺���̗̈�ł��B
�t�ɁA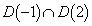 ���̓_���A
���̓_���A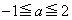 �������ׂĂ�a�ɑ���
�������ׂĂ�a�ɑ���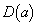 �̓_�ɂȂ邱�Ƃׂ܂��B
�̓_�ɂȂ邱�Ƃׂ܂��B
����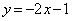 �ƒ���
�ƒ���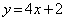 �̌�_�́A
�̌�_�́A �ƂȂ�A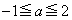 �̂Ƃ��A�_
�̂Ƃ��A�_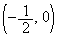 �́A�̈�
�́A�̈�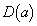 ���̓_�ł��B
���̓_�ł��B �@�̋��E���F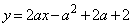 �@����A
�@����A
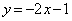 �@����B
�@����B �A�ƇB��A������ƁA
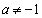 �ł���A
�ł���A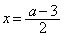 �C
�C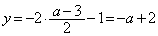
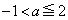 �ɂ����ẮA
�ɂ����ẮA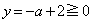 ���A�A�ƇB�̌�_��x������㑤�ɂ���܂��B
���A�A�ƇB�̌�_��x������㑤�ɂ���܂��B
�A�ƁA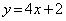 �@����C
�@����C��A������ƁA
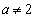 �ł���A
�ł���A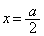 �C
�C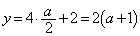
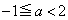 �ɂ����ẮA
�ɂ����ẮA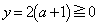 ���A�A�ƇC�̌�_��x������㑤�ɂ���܂��B
���A�A�ƇC�̌�_��x������㑤�ɂ���܂��B
�]���āA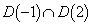 ���̓_�́A
���̓_�́A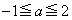 �������ׂĂ�a�ɑ���
�������ׂĂ�a�ɑ���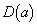 �̓_�ɂȂ�܂��B�܂�A
�̓_�ɂȂ�܂��B�܂�A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B