阪大理系数学'13年前期[3]
4個の実数
がすべて素数となるような正の整数nは存在しない。これを証明せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 ぱっと見には方針が立ちませんが，素数を2と2以外に分けると、偶数か奇数か、ということになり、それなら、3の倍数かどうかと調べてゆくと、嫌でも解決してしまいます。なお、整数を参照してください。
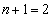だとすると、
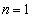です。このとき、
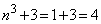ですが、これは素数ではありません。
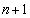が3以上の素数だとすると、
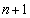は奇数でnは偶数です。
このとき、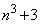
，
，
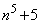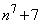はいずれも奇数で、素数の可能性があり、偶奇を考えるだけでは題意を示すことができません。
そこで、nが3の倍数かどうかを考えてみます。
(i) nは偶数なのでkを偶数として、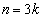
のとき、
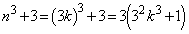は3の倍数で素数ではありません。 (ii) kを奇数として、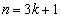
のとき、 
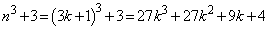は3の倍数ではなく、素数の可能性があります。
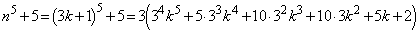は3の倍数なので素数ではありません。(iii) kを偶数として、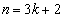
のとき、 
，
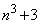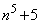は3の倍数ではなく、素数の可能性がありますが、
は3の倍数なので素数ではありません。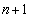
，
，
，
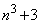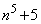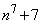がすべて素数となるような正の整数nは存在しません。(証明終)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，
，