��嗝�n���w'22�N�O��[1]
r�𐳂̎����Ƃ���B���f�����ʏ�ŁA�_z���_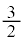 �𒆐S�Ƃ��锼�ar�̉~������Ƃ��A
�𒆐S�Ƃ��锼�ar�̉~������Ƃ��A
�����_w���`���}�`�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�p�o�^�C�v�̕��f�����ʏ�̕ϊ��̖��ł��B�Ȃ��A���f���̐}�`�I���p���Q�Ƃ��Ă��������B
�_z���_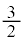 �𒆐S�Ƃ��锼�ar�̉~������̂ŁA
�𒆐S�Ƃ��锼�ar�̉~������̂ŁA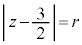 �@����@
�@����@
�^���F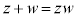 �ɂ����āA
�ɂ����āA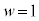 �Ƃ���ƁA
�Ƃ���ƁA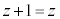 �ƂȂ萬�����Ȃ��̂�
�ƂȂ萬�����Ȃ��̂�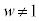 �C���̂Ƃ��A
�C���̂Ƃ��A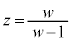
������@�ɑ������ƁA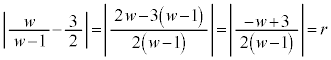 �@��
�@�� 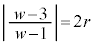 �@����A
�@����A
w�́A�_1�Ƃ̋����A�_3�Ƃ̋����̔䂪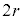 �F1�ƂȂ�_�ł��B
�F1�ƂȂ�_�ł��B
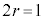 �C�܂�
�C�܂�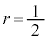 �̂Ƃ��ɂ́A�_1 �Ɠ_3���瓙�����̓_�A�܂�Aw�̕`���}�`�́A�_1�Ɠ_3�����Ԑ����̐��������A�����A�_2��ʂ�����ɐ����Ȓ����ɂȂ�܂��B
�̂Ƃ��ɂ́A�_1 �Ɠ_3���瓙�����̓_�A�܂�Aw�̕`���}�`�́A�_1�Ɠ_3�����Ԑ����̐��������A�����A�_2��ʂ�����ɐ����Ȓ����ɂȂ�܂��B
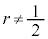 �̂Ƃ��ɂ́A�A�|���j�E�X�̉~�ɂȂ�܂��B���̂Ƃ��A
�̂Ƃ��ɂ́A�A�|���j�E�X�̉~�ɂȂ�܂��B���̂Ƃ��A
�_3�Ɠ_1��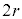 �F1�ɓ�������_P�́A
�F1�ɓ�������_P�́A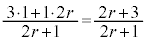
�_3�Ɠ_1��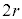 �F1�ɊO������_Q�́A
�F1�ɊO������_Q�́A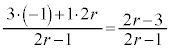
w�̕`���}�`�́A�_P�C�_Q�a�̗��[�Ƃ���~�ŁA���̒��S�́A����PQ�̒��_�ł����āA
���a�́APQ��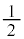 �ł����āA
�ł����āA
����āAw�̕`���}�`�́A
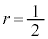 �̂Ƃ��A�_2��ʂ�����ɐ����Ȓ����B
�̂Ƃ��A�_2��ʂ�����ɐ����Ȓ����B
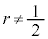 �̂Ƃ��A�_
�̂Ƃ��A�_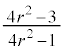 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a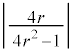 �̉~ �c�c[��]
�̉~ �c�c[��]
�ʉ��D�A����v�Z�ŋ��߂�ꍇ�́A�A�̕�����ė��ӂ�2�悵�A
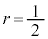 �̂Ƃ��A
�̂Ƃ��A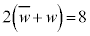 �@��
�@�� 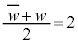 �����w�̎�����2�ł��Bw�͓_2��ʂ�����ɐ����Ȓ�����̓_�ł��B
�����w�̎�����2�ł��Bw�͓_2��ʂ�����ɐ����Ȓ�����̓_�ł��B
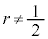 �̂Ƃ��A
�̂Ƃ��A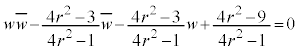
����́A�_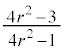 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a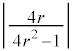 �̉~�ł��B
�̉~�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 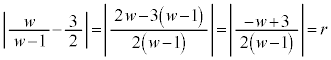 �@��
�@�� 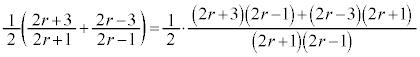
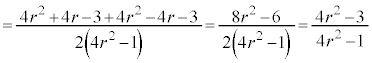
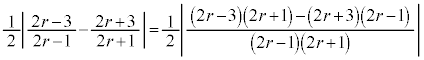
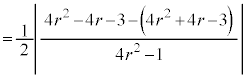
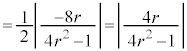
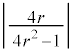 �̉~ �c�c[��]
�̉~ �c�c[��]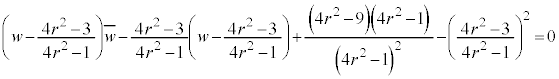
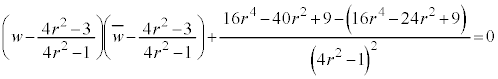
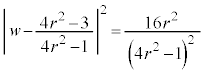
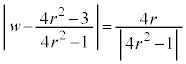
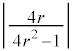 �̉~�ł��B
�̉~�ł��B