大阪大学理系2022年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] rを正の実数とする。複素数平面上で、点zが点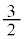
を中心とする半径rの円周上を動くとき、
を満たす点wが描く図形を求めよ。
[解答へ]
[2]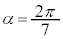 
とする。以下の問いに答えよ。
(1) 
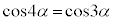であることを示せ。 (2) 
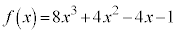とするとき、
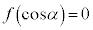が成り立つことを示せ。 (3) 
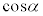は無理数であることを示せ。 [解答へ]
[3] 正の実数t に対し、座標平面上の2点P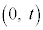
とQ
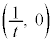を考える。t が
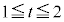の範囲を動くとき、座標平面内で線分PQが通過する部分を図示せよ。
[解答へ]
[4]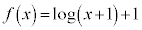 
とする。以下の問いに答えよ。
(1) 方程式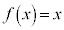
は、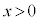
の範囲でただ1つの解をもつことを示せ。 (2) (1)の解をαとする。実数xが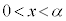
を満たすならば、次の不等式が成り立つことを示せ。 (3) 数列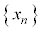
を で定める。このとき、すべての自然数nに対して、
が成り立つことを示せ。
(4) (3)の数列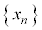
について、
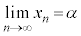を示せ。 [解答へ]
[5] 座標平面において、t を媒介変数として
で表される曲線をCとする。曲線Cとx軸で囲まれた部分の面積を求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
(
)
，
(
)