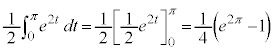��嗝�n���w'22�N�O��[5]
���W���ʂɂ����āAt ��}��ϐ��Ƃ���
�ŕ\�����Ȑ���C�Ƃ���B�Ȑ�C��x���ň͂܂ꂽ�����̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�}��ϐ��\�����ꂽ���̃O���t�̖ʐς��v�Z������ł��B�Ȃ��A��ϕ��Ɩʐ�(2)���Q�Ƃ��Ă��������B
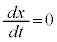 �Ƃ���ƁA
�Ƃ���ƁA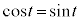 �C
�C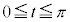 �ɂ����Ă�
�ɂ����Ă�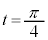
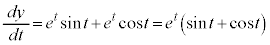 �@����A
�@����A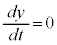 �Ƃ���ƁA
�Ƃ���ƁA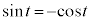 �C
�C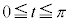 �ɂ����Ă�
�ɂ����Ă�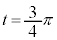
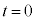 �̂Ƃ��A
�̂Ƃ��A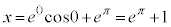 �C
�C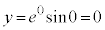
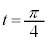 �̂Ƃ��A
�̂Ƃ��A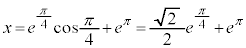 (
(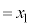 �Ƃ����܂�)�C
�Ƃ����܂�)�C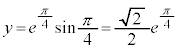 (
(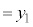 �Ƃ����܂�)
�Ƃ����܂�)
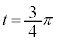 �̂Ƃ��A
�̂Ƃ��A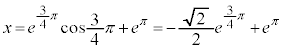 (
(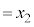 �Ƃ����܂�)�C
�Ƃ����܂�)�C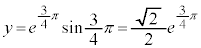 (
(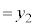 �Ƃ����܂�)
�Ƃ����܂�)
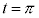 �̂Ƃ��A
�̂Ƃ��A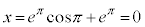 �C
�C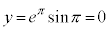
�����\�́A�ȉ��̂悤�ɂȂ�܂��B
| t | 0 | �@ | 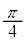 | �@ | 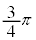 | �@ | π |
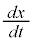 | �{ | �{ | 0 | �| | �| | �| | �| |
| x | 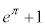 |  | 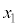 |  | 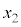 |  | 0 |
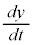 | �{ | �{ | �{ | �{ | 0 | �| | �| |
| y | 0 |  | 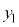 |  | 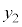 |  | 0 |
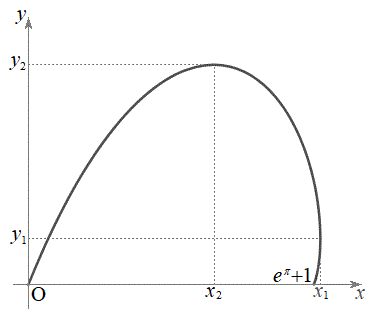 �����\���A�Ȑ�C (�O���t�͉E�}�A��X�̊��̃O���t(7)���Q��)��x���ň͂܂ꂽ�����̖ʐ�S�́A�Ȑ�C��
�����\���A�Ȑ�C (�O���t�͉E�}�A��X�̊��̃O���t(7)���Q��)��x���ň͂܂ꂽ�����̖ʐ�S�́A�Ȑ�C��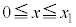 �̕�����x���̊Ԃɋ��܂ꂽ�����̖ʐς���A�Ȑ�C��
�̕�����x���̊Ԃɋ��܂ꂽ�����̖ʐς���A�Ȑ�C��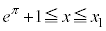 �̕�����x���̊Ԃɋ��܂ꂽ�����̖ʐς����������̂ł��B
�̕�����x���̊Ԃɋ��܂ꂽ�����̖ʐς����������̂ł��B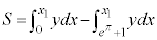
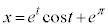 �Ƃ����ƁA�@���
�Ƃ����ƁA�@���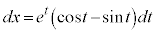
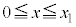 �ɂ����ẮAx�F
�ɂ����ẮAx�F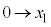 �̂Ƃ�t�F
�̂Ƃ�t�F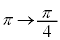
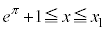 �ɂ����ẮAx�F
�ɂ����ẮAx�F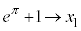 �̂Ƃ�t�F
�̂Ƃ�t�F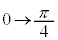
��1���̐ϕ���(�s��ϕ��̌������Q��)�A
��2���̐ϕ���(�����ϕ��@���Q��)�A
���A
�� 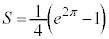 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B