��X�̊��̃O���t(7)�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A�����̌����A���̑����A���̉������Q�Ƃ��Ă��������B
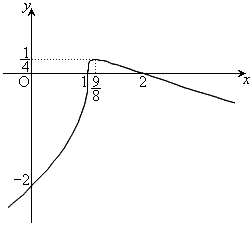 ��D�}��ϐ��\�����ꂽ��
��D�}��ϐ��\�����ꂽ��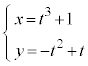 �@(t�͑S����)�̃O���t
�@(t�͑S����)�̃O���t
�c�嗝�H��'95�N�ɏo�肳�ꂽ���ł��B
t���S�������Ƃ�Ƃ��Ax���S����(��`��)���Ƃ�܂��By�͈̔͂́A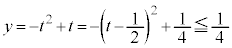 ���A
���A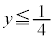 �@(�l��)
�@(�l��)
x�Cy�����ꂼ��t�Ŕ�������ƁA
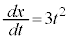
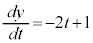
�}��ϐ��\�����ꂽ���̔����@���A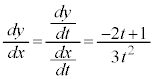 �@����@�@(
�@����@�@(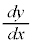 ��x�ŕ\�������K�v�͂���܂���)
��x�ŕ\�������K�v�͂���܂���)
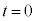 �̂Ƃ��A
�̂Ƃ��A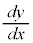 ����`�ł��Ȃ��̂ł����A���̂Ƃ��A
����`�ł��Ȃ��̂ł����A���̂Ƃ��A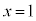 �C
�C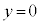 (�_
(�_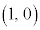 �ɂ�����ڐ���x���ɐ����ɂȂ�܂�)
�ɂ�����ڐ���x���ɐ����ɂȂ�܂�)
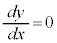 �Ƃ���ƁA
�Ƃ���ƁA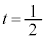 �C���̂Ƃ��A
�C���̂Ƃ��A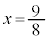 �C
�C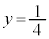 (�ɑ�l)
(�ɑ�l)
�}��ϐ��\�����ꂽ����2���̓���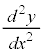 ���ǂ̂悤�ɋ��߂邩�A���ɂȂ邱�Ƃ�����܂��B
���ǂ̂悤�ɋ��߂邩�A���ɂȂ邱�Ƃ�����܂��B
�@���́At�̊��̌`�ɕ\����Ă���̂ŁA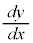 ��x�Ŕ������邱�Ƃ��ł��܂���B�������At�ɂ��ĂȂ�����ł��܂��B
��x�Ŕ������邱�Ƃ��ł��܂���B�������At�ɂ��ĂȂ�����ł��܂��B
�����ŁA�������̔����@�ɂ��A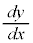 ��t�Ŕ����������̂ɁA
��t�Ŕ����������̂ɁA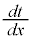 �������āA
�������āA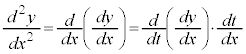 �Ƃ��܂��B
�Ƃ��܂��B
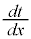 �́At��x�̎��ŕ\���Ĕ��������肵�Ȃ��Ă��A�t���̔����@�ɂ��A
�́At��x�̎��ŕ\���Ĕ��������肵�Ȃ��Ă��A�t���̔����@�ɂ��A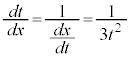 �Ƃ���悢�̂ł��B
�Ƃ���悢�̂ł��B
�@�����ӂ�t�Ŕ�������ƁA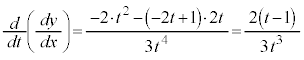
���ǁA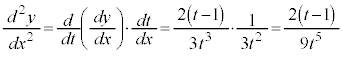
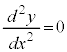 �Ƃ���ƁA
�Ƃ���ƁA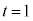 �ƂȂ�܂����A���̂Ƃ��A
�ƂȂ�܂����A���̂Ƃ��A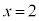 �C
�C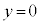 �ł��B
�ł��B
�ȏ���A�����\�����܂����A�}��ϐ��\�����ꂽ���̏ꍇ�A�����\�̏������Ɍl��������A�l�ɂ���āA�Q�l���ɂ���āA���܂��܂ȏ�����������܂��B���ꂼ��꒷��Z�������āA���̗v���ɍ��킹�Ďg����������Ƃ悢�̂ł����A���̃E�F�u�E�T�C�g�ł́A���L�̏������œ��ꂵ�܂��B
��ԏ�̗��ɁA�}��ϐ��̓������A������������傫�����������ď����܂��B
���̗��ɁA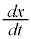 �̐����Ȃǂׂď������݂܂��B
�̐����Ȃǂׂď������݂܂��B
���̉��ɁA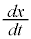 �̐����ɍ��킹�āAx�̑����A�ɒl�Ȃǂ��������݂܂��B
�̐����ɍ��킹�āAx�̑����A�ɒl�Ȃǂ��������݂܂��B
���̉��ɁA�ʏ�̑����\�Ɠ������A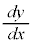 �C
�C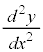 �Cy�̓����������Ă䂫�܂��B
�Cy�̓����������Ă䂫�܂��B
���̏������ł́A�ꊇ���āAt�Cx�Cy�̓��������Ă䂯��̂ł����A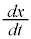 �����̒l���Ƃ�Ƃ��ɁAx��������������傫�����֕����ɁA�傫�������珬�������������ĕ��ԕ������ł��Ă��܂��A�����\���E���獶�Ɍ������Č���K�v������ϑ��I�ȏꍇ���o�Ă��܂��B
�����̒l���Ƃ�Ƃ��ɁAx��������������傫�����֕����ɁA�傫�������珬�������������ĕ��ԕ������ł��Ă��܂��A�����\���E���獶�Ɍ������Č���K�v������ϑ��I�ȏꍇ���o�Ă��܂��B
���̗�ł́A�킩��₷���悤�ɁA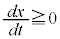 �ƂȂ��āAx��������������傫�����֕��Ԋ������グ�Ă���܂����A����̓������(�e93�N���n�O��[6])�ł́Ax���t�ɕ��ԂƂ��낪�o�Ă���悤�Ȋ��������܂��B
�ƂȂ��āAx��������������傫�����֕��Ԋ������グ�Ă���܂����A����̓������(�e93�N���n�O��[6])�ł́Ax���t�ɕ��ԂƂ��낪�o�Ă���悤�Ȋ��������܂��B
�O���t�͉E��Ɏ����܂����B
| t |
| 0 |
| 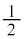 |
| 1 |
|
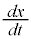 | �{ | 0 | �{ | �{ | �{ | �{ | �{ |
| x |  | 1 |  | 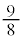 |  | 2 |  |
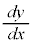 | �{ | �~ | �{ | 0 | �| | �| | �| |
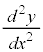 | �{ | �~ | �| | �| | �| | 0 | �{ |
| y |  | 0 | 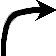 | 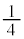 | 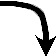 | 0 |  |
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 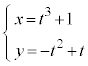 �@
�@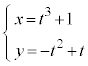 �@(t�͑S����)�̃O���t
�@(t�͑S����)�̃O���t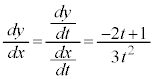 �@����@�@(
�@����@�@(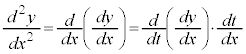 �Ƃ��܂��B
�Ƃ��܂��B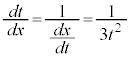 �Ƃ���悢�̂ł��B
�Ƃ���悢�̂ł��B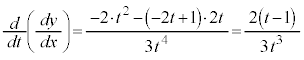
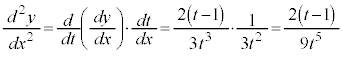
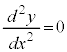 �Ƃ���ƁA
�Ƃ���ƁA