��嗝�n���w'22�N�O��[3]
���̎���t �ɑ��A���W���ʏ��2�_P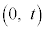 ��Q
��Q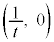 ���l����Bt ��
���l����Bt ��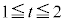 �͈̔͂��Ƃ��A���W���ʓ��Ő���PQ���ʉ߂��镔����}������B
�͈̔͂��Ƃ��A���W���ʓ��Ő���PQ���ʉ߂��镔����}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���������A�Ȑ��̒ʉߔ͈͂����߂���́A��֑�ł͕p�o�e�[�}�ł��B
2�_P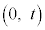 ��Q
��Q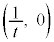 ��ʂ������̕������́A
��ʂ������̕������́A
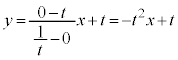 �@(
�@(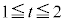 )�@����@
)�@����@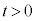 ��P��y�����
��P��y�����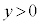 �̕����Ɉʒu����_�AQ��x�����
�̕����Ɉʒu����_�AQ��x�����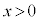 �̕����Ɉʒu����_�Ȃ̂ŁA�����@�̂����A����PQ��ɗ��镔���́A
�̕����Ɉʒu����_�Ȃ̂ŁA�����@�̂����A����PQ��ɗ��镔���́A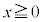 ����
����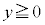 �̕����̒��ɂ���܂��B�@���(��)
�̕����̒��ɂ���܂��B�@���(��)
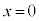 �̂Ƃ�
�̂Ƃ�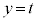 �C
�C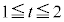 ���
��� �@����A
�@����A
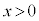 �̂Ƃ��A�@��t��2�����Ƃ݂�ƁA
�̂Ƃ��A�@��t��2�����Ƃ݂�ƁA
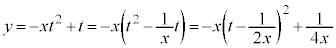 (
(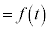 �Ƃ����܂�)
�Ƃ����܂�)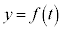 �̃O���t�́A����
�̃O���t�́A����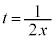 �ɂ���������ł��B
�ɂ���������ł��B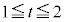 �Ȃ̂ŁA
�Ȃ̂ŁA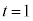 �C
�C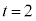 �C
�C (
(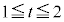 �͈̔͂̒��ԓ_)�Ǝ��̈ʒu
�͈̔͂̒��ԓ_)�Ǝ��̈ʒu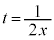 �Ƃ̑召�W�ŏꍇ�������܂�(2�����̍ő�E�ŏ����Q��)�B
�Ƃ̑召�W�ŏꍇ�������܂�(2�����̍ő�E�ŏ����Q��)�B
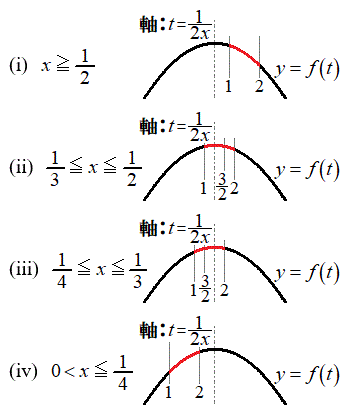 (i)
(i) 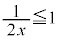 �̂Ƃ�
�̂Ƃ�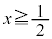 �C(ii)
�C(ii) 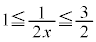 �̂Ƃ�
�̂Ƃ�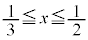 �C(iii)
�C(iii) 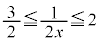 �̂Ƃ�
�̂Ƃ�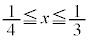 �C(iv)
�C(iv) 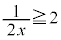 �̂Ƃ�
�̂Ƃ�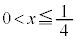 �C���ꂼ��̏ꍇ�ɉ����āA
�C���ꂼ��̏ꍇ�ɉ����āA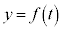 �̃O���t�͉E�}�̂悤�ɂȂ�܂��B
�̃O���t�͉E�}�̂悤�ɂȂ�܂��B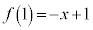 �C
�C �C
�C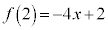 �ł��B
�ł��B
(i) 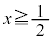 �̂Ƃ��A
�̂Ƃ��A �ŁAt �͈̔�
�ŁAt �͈̔�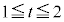 �͎��̉E���ɗ��܂��B
�͎��̉E���ɗ��܂��B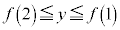 �C(��)��
�C(��)��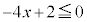 ���A
���A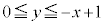 �@����B
�@����B �������A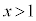 �ɂ����Ă�
�ɂ����Ă�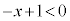 �Ȃ̂ŁA����PQ�̒ʉߔ͈͂����݂���̂�
�Ȃ̂ŁA����PQ�̒ʉߔ͈͂����݂���̂�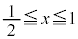 �͈̔͂����ł��B
�͈̔͂����ł��B (ii) 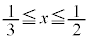 �̂Ƃ��A
�̂Ƃ��A �ŁAt �͈̔�
�ŁAt �͈̔�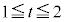 �͎��̈ʒu���܂�
�͎��̈ʒu���܂�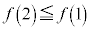 �C
�C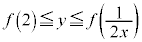 ���A
���A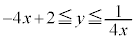 �@����C
�@����C (iii) 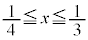 �̂Ƃ��A
�̂Ƃ��A �ŁAt �͈̔�
�ŁAt �͈̔�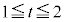 �͎��̈ʒu���܂�
�͎��̈ʒu���܂�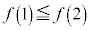 �C
�C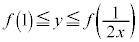 ���A
���A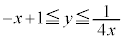 �@����D
�@����D 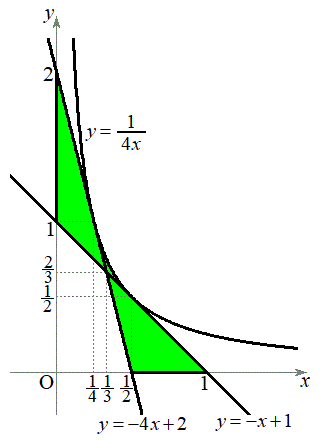 ����
����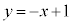 ��
��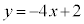 �́A
�́A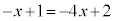 �Ƃ����
�Ƃ���� �C
�C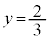 ���A
���A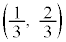 �ɂ����Č����܂��B
�ɂ����Č����܂��B
����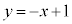 ��
��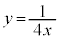 �́A
�́A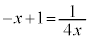 �Ƃ����
�Ƃ����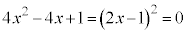 �C
�C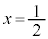 �C
�C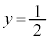 ���A
���A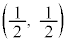 �ɂ����Đڂ��܂��B
�ɂ����Đڂ��܂��B
����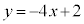 ��
��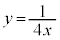 �́A
�́A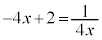 �Ƃ����
�Ƃ����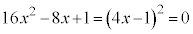 �C
�C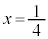 �C
�C ���A
���A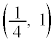 �ɂ����Đڂ��܂��B
�ɂ����Đڂ��܂��B
����PQ���ʉ߂��镔����}������(�s�����̕\���̈����Q��)�ƁA�A�C�B�C�C�C�D�C�E���A�E�}���ΐF���F��(���E�����܂�)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 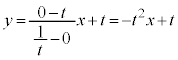 �@(
�@(