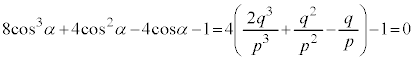��嗝�n���w'22�N�O��[2]
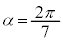 �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) 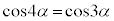 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (2) 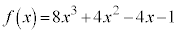 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A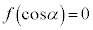 �����藧���Ƃ������B
�����藧���Ƃ������B (3) 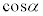 �͖������ł��邱�Ƃ������B
�͖������ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@n�����R���Ƃ��āA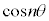 ��
��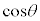 �̑������ŕ\�������̂�
�̑������ŕ\�������̂�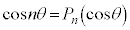 �Ƃ��āA������
�Ƃ��āA������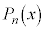 ���`�F�r�V�F�t�̑������ƌ����܂��B
���`�F�r�V�F�t�̑������ƌ����܂��B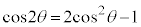 �C
�C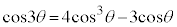 �C
�C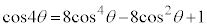 ���A
���A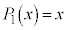 �C
�C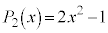 �C
�C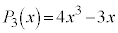 �C
�C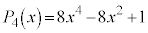 �ł��B
�ł��B
(1) 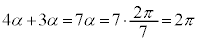 ���A
���A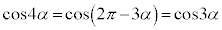 �@(�O�p�����Q��)
�@(�O�p�����Q��)
(2) 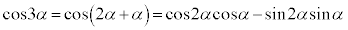 �@(���@�藝���Q��)
�@(���@�藝���Q��)
(1)���A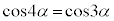 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA ����āA
(3) �w���@�Ŏ����܂��B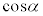 ���L�������Ɖ��肵�Ap�Cq���݂��ɑf�Ȏ��R���Ƃ��āA
���L�������Ɖ��肵�Ap�Cq���݂��ɑf�Ȏ��R���Ƃ��āA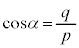 �Ƃ�����Ƃ��܂��B
�Ƃ�����Ƃ��܂��B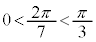 ���A
���A �ł����āA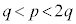 �@����A�@�ł��B�@���A
�@����A�@�ł��B�@���A q�C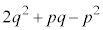 �Cp�������Ȃ̂ŁAp��q�̔{���ƂȂ�p�Cq���݂��ɑf�ł��邱�Ƃ���
�Cp�������Ȃ̂ŁAp��q�̔{���ƂȂ�p�Cq���݂��ɑf�ł��邱�Ƃ���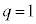 �Ɍ����܂��B����ƇA���A
�Ɍ����܂��B����ƇA���A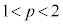 �ƂȂ�܂����A����������R��p�͑��݂��܂���B�܂�
�ƂȂ�܂����A����������R��p�͑��݂��܂���B�܂�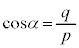 �Ƃ�����Ƃ�������ɖ������܂��B�����
�Ƃ�����Ƃ�������ɖ������܂��B�����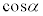 ��L�����Ƃ�������͌��ŁA
��L�����Ƃ�������͌��ŁA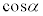 �͖������ł��B
�͖������ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B