��嗝�n���w'22�N�O��[4]
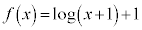 �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) ������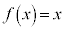 �́A
�́A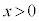 �͈̔͂ł���1�̉��������Ƃ������B
�͈̔͂ł���1�̉��������Ƃ������B (2) (1)�̉���α�Ƃ���B����x��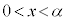 �����Ȃ�A���̕s���������藧���Ƃ������B
�����Ȃ�A���̕s���������藧���Ƃ������B (3) ����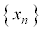 ��
�� �Œ�߂�B���̂Ƃ��A���ׂĂ̎��R��n�ɑ��āA
�����藧���Ƃ������B
(4) (3)�̐���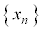 �ɂ��āA
�ɂ��āA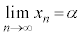 �������B
�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�K���������ϒl�̒藝�������o���Ȃ��Ă��悢�̂ł����A���ϒl�̒藝�𗘗p���ē��Ă��X�b�L���������Ƃ��ł����Ԃ̋Ɍ��l�̖��ł��B
����āA������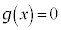 �C�܂�
�C�܂�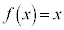 �́A
�́A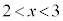 �͈̔͂ɂ���1�̉��������܂�(���Ԓl�̒藝���Q��)�B
�͈̔͂ɂ���1�̉��������܂�(���Ԓl�̒藝���Q��)�B
(2) (1)�̉���α�Ƃ���(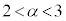 )��
)��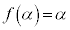 �ł���A
�ł���A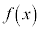 �͕��ϒl�̒藝�̗v�������̂ŁA���ϒl�̒藝���A
�͕��ϒl�̒藝�̗v�������̂ŁA���ϒl�̒藝���A 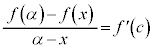 �@(
�@(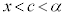 )�@����@
)�@����@��������c�����݂��܂��B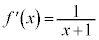 ���
��� �ł����A
�ł����A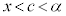 ���
���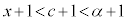 �C
�C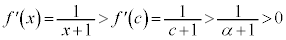
�@��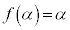 ���A
���A
(3) n�����R���Ƃ��āA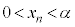 ���Ƃ���A
���Ƃ���A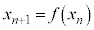 ���A(2)�̕s������x��
���A(2)�̕s������x��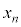 �Ƃ��āA
�Ƃ��āA 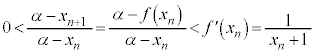 �@����A
�@����A�������܂��B
�����ŁA�A���玦���ׂ��s�����̌`����邽�߂ɂ́A�܂��A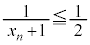 �܂�
�܂�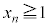 �Ƃ������킯�ł��B�����ŁA
�Ƃ������킯�ł��B�����ŁA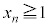 (
(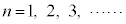 )�����w�I�A�[�@�Ŏ����܂��B
)�����w�I�A�[�@�Ŏ����܂��B
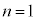 �̂Ƃ��A
�̂Ƃ��A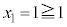 ��萬�藧���܂��B
��萬�藧���܂��B
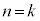 �̂Ƃ��A
�̂Ƃ��A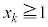 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA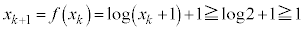 ���A
���A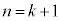 �̂Ƃ������藧���܂��B
�̂Ƃ������藧���܂��B
����āA���w�I�A�[�@���A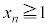 (
(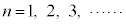 )�����藧���܂��B
)�����藧���܂��B
������A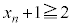 �C
�C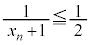 �@����B�@�ƂȂ�܂��B
�@����B�@�ƂȂ�܂��B
�܂��A�A�������邽�߂ɂ́A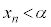 �������K�v������܂��B�����ŁA
�������K�v������܂��B�����ŁA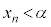 �����w�I�A�[�@�Ŏ����܂��B
�����w�I�A�[�@�Ŏ����܂��B
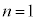 �̂Ƃ��A
�̂Ƃ��A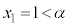 (��
(�� 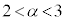 )��萬�藧���܂��B
)��萬�藧���܂��B
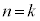 �̂Ƃ��A
�̂Ƃ��A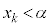 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA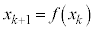 �ł����āA(2)�̕s������x��
�ł����āA(2)�̕s������x��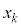 �Ƃ��āA
�Ƃ��āA 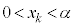 ���A
���A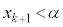 �ƂȂ�A
�ƂȂ�A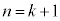 �̂Ƃ������藧���܂��B
�̂Ƃ������藧���܂��B
����āA���w�I�A�[�@���A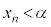 (
(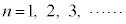 )�����藧���܂��B
)�����藧���܂��B
�ȏ���A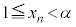 �ƂȂ�̂ŁA�A�������āA�B���A���ׂĂ̎��R��n�ɂ��āA
�ƂȂ�̂ŁA�A�������āA�B���A���ׂĂ̎��R��n�ɂ��āA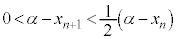 �@����C�@�����藧���܂��B
�@����C�@�����藧���܂��B
(4) �C���A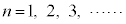 �Ƃ��ČJ��Ԃ��g���ƁA
�Ƃ��ČJ��Ԃ��g���ƁA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 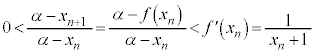 �@����A
�@����A