���Ԓl�̒藝�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���Ԓl�̒藝�F���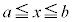 �ɂ������A���Ȋ�
�ɂ������A���Ȋ�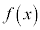 �ɂ��āA
�ɂ��āA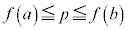 �C�܂��́A
�C�܂��́A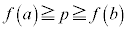 ����p�ɑ��āA
����p�ɑ��āA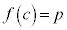 �C
�C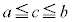 ����c�����݂���B
����c�����݂���B
[�ؖ�]�E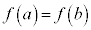 �̂Ƃ��́A
�̂Ƃ��́A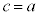 �܂���
�܂���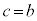 �Ƃ���悢�̂Ŗ��炩�B
�Ƃ���悢�̂Ŗ��炩�B
�E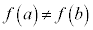 �̂Ƃ��A
�̂Ƃ��A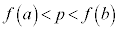 �Ƃ��āA
�Ƃ��āA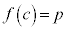 �C
�C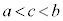 �ƂȂ�c��(
�ƂȂ�c��(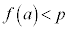 �C
�C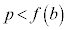 ���A
���A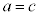 �Ƃ�
�Ƃ�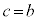 �Ƃ������Ƃ͂��蓾�Ȃ�)���݂��Ȃ��@����@�@�Ɖ��肵�܂��B
�Ƃ������Ƃ͂��蓾�Ȃ�)���݂��Ȃ��@����@�@�Ɖ��肵�܂��B
�����ŁA��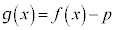 �Ƃ��Ċ�
�Ƃ��Ċ�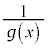 ���l����ƁA
���l����ƁA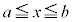 �ɂ����āA
�ɂ����āA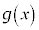 �͘A���Ȋ��ł���A
�͘A���Ȋ��ł���A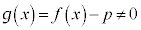 �Ȃ̂ŁA
�Ȃ̂ŁA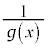 ���܂��A���Ȋ��ł��B
���܂��A���Ȋ��ł��B
�ő�l�E�ŏ��l�̒藝�ɂ��A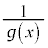 �́A
�́A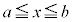 �ɂ����āA�ő�l�A�ŏ��l�������܂��B
�ɂ����āA�ő�l�A�ŏ��l�������܂��B
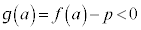 �C
�C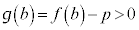 ���A
���A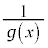 �͐��̒l�����̒l���Ƃ���ł��B�]���āA
�͐��̒l�����̒l���Ƃ���ł��B�]���āA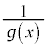 �̍ő�lM��
�̍ő�lM��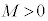 �ł���A�ŏ��lm��
�ł���A�ŏ��lm��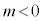 �ł��B
�ł��B
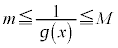 ���A
���A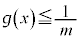 ����
����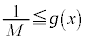 �C�ł����āA�܂�A
�C�ł����āA�܂�A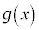 �́A
�́A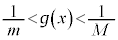 �ƂȂ�l���Ƃ蓾�܂���(
�ƂȂ�l���Ƃ蓾�܂���(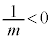 �ɒ���)�B
�ɒ���)�B
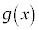 �͐��̒l�����̒l���Ƃ���ł���A
�͐��̒l�����̒l���Ƃ���ł���A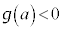 �C
�C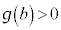 ���A
���A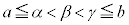 �ł����āA
�ł����āA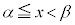 �ɂ�����
�ɂ�����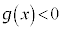 �C
�C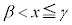 �ɂ�����
�ɂ�����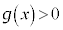 �ƂȂ�α�Cβ�Cγ���K�����݂��܂�(���m�ɂ́A�������f�������O��ɂȂ��Ă��܂�)�B
�ƂȂ�α�Cβ�Cγ���K�����݂��܂�(���m�ɂ́A�������f�������O��ɂȂ��Ă��܂�)�B
���̂Ƃ��A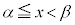 �ɂ�����
�ɂ�����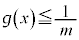 ���A
���A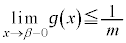 �C�܂��A
�C�܂��A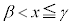 �ɂ�����
�ɂ�����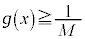 ���A
���A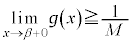
�� 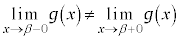
����́A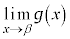 �����݂��Ȃ����ƁA����ɁA
�����݂��Ȃ����ƁA����ɁA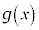 �C����
�C����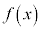 ��
��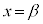 �ɂ����ĘA���łȂ����Ƃ��Ӗ����Ă���A
�ɂ����ĘA���łȂ����Ƃ��Ӗ����Ă���A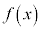 ��
��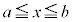 �ɂ����ĘA���ł��邱�Ƃɔ����܂��B
�ɂ����ĘA���ł��邱�Ƃɔ����܂��B
����āA����@�͌��ł��B
�]���āA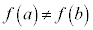 �̂Ƃ��A
�̂Ƃ��A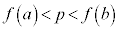 �Ƃ��āA
�Ƃ��āA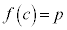 �C
�C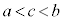 �ƂȂ�c�����݂��܂��B
�ƂȂ�c�����݂��܂��B
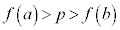 �̏ꍇ�����l�ł��B�@(�ؖ��I)
�̏ꍇ�����l�ł��B�@(�ؖ��I)
��D�������F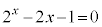 ��
��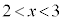 �͈̔͂Ɏ������������Ƃ������B
�͈̔͂Ɏ������������Ƃ������B
[��]�@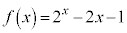 �Ƃ����ƁA
�Ƃ����ƁA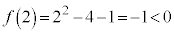 �C
�C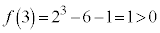
���Ԓl�̒藝�ɂ��A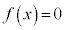 �́A
�́A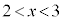 �͈̔͂Ɏ������������܂��B
�͈̔͂Ɏ������������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B