��嗝�n���w'23�N�O��[2]
���ʏ��3�_O�CA�CB��
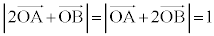 �@���@
�@���@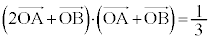
(1) 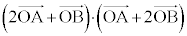 �����߂�B
�����߂�B (2) ���ʏ�̓_P��
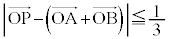 �@���@
�@���@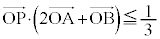
���݂����悤�ɓ����Ƃ��A �̍ő�l�ƍŏ��l�����߂�B
�̍ő�l�ƍŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����v�Z�̖��ł��B��X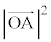 �Ƃ�
�Ƃ�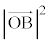 �Ə����͖̂ʓ|�Ȃ̂ŁA������ɒu�������܂��傤�B
�Ə����͖̂ʓ|�Ȃ̂ŁA������ɒu�������܂��傤�B
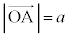 (
(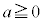 )�C
)�C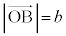 (
(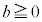 )�C
)�C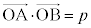 �Ƃ����ƁA
�Ƃ����ƁA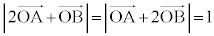 ���A
���A
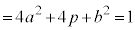 �@����@
�@����@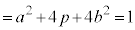 �@����A
�@����A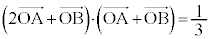 ���A
���A
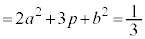 �@����B
�@����B
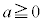 �C
�C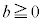 ���A
���A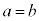
�@�ɑ������ƁA
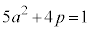 �@����C
�@����C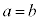 ���B�ɑ������ƁA
���B�ɑ������ƁA
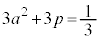 �@����D
�@����D
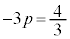 �@��
�@�� 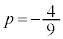
(1) 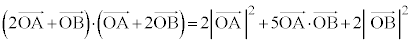
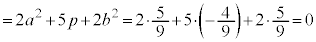 ......[��]
......[��]������A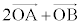 ��
��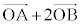
�����ňȍ~�́A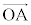 �C
�C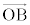 ����ɂ��čl����̂ł͂Ȃ��A
����ɂ��čl����̂ł͂Ȃ��A 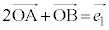 �@����E�C
�@����E�C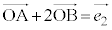 �@����F
�@����F�Ƃ����āA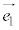 �C
�C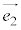 ����ɂ��čl���邱�Ƃɂ��܂��B
����ɂ��čl���邱�Ƃɂ��܂��B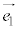 ��
��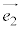 �ł��B�܂��A��蕶���
�ł��B�܂��A��蕶���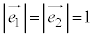 �@����G�@�ł��B
�@����G�@�ł��B ���D�ŏ�����E�C�F�̂悤�ɂ����A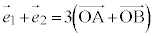 �Ȃ̂ŁA��蕶����
�Ȃ̂ŁA��蕶����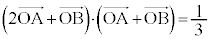 �͇G���g���āA
�͇G���g���āA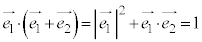 �ƂȂ�A
�ƂȂ�A �������ɋ��߂��܂��B
�������ɋ��߂��܂��B
(2)��蕶�̍ŏ��̏����F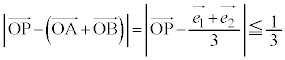 ���AP�́A
���AP�́A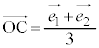 �Œ�܂�_C�𒆐S�Ƃ��锼�a
�Œ�܂�_C�𒆐S�Ƃ��锼�a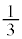 �̉~C��(�~������܂ށB�E�}�Q�ƁA�~C��
�̉~C��(�~������܂ށB�E�}�Q�ƁA�~C��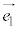 �C
�C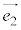 �̑o���ɐڂ��邱�Ƃɒ���)�̓_�ł��B
�̑o���ɐڂ��邱�Ƃɒ���)�̓_�ł��B
�E��p���āA(2)��蕶�̂��Ƃ̏����F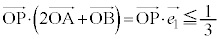 ���l���܂��B�G��
���l���܂��B�G��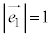 ���A
���A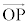 ��
��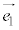 �̂Ȃ��p��θ�Ƃ��āA
�̂Ȃ��p��θ�Ƃ��āA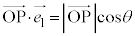 (�������Q��)�́A�_P����
(�������Q��)�́A�_P����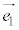 �ɉ��낵��������PH�Ƃ��āA
�ɉ��낵��������PH�Ƃ��āA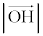 �C�܂�A
�C�܂�A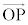 ��
��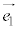 �̕����ւ̐��ˉe�̒����ł��B
�̕����ւ̐��ˉe�̒����ł��B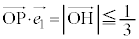 ���A�E�}�ŁA
���A�E�}�ŁA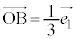 �Œ�܂�_��B�CB��ʂ�
�Œ�܂�_��B�CB��ʂ�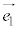 �ɐ����Ȓ����Ɖ~C�Ƃ�2��_�̂���B�łȂ�����A�Ƃ��āA�~C���̓_�̈ʒu�x�N�g��
�ɐ����Ȓ����Ɖ~C�Ƃ�2��_�̂���B�łȂ�����A�Ƃ��āA�~C���̓_�̈ʒu�x�N�g��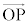 ��
��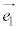 �����ւ̐��ˉe��
�����ւ̐��ˉe��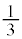 �ȉ��ɂȂ�̂́A�E�}�ŊD�F�ɒ��F��������(�~C���̒��aAB���獶���̔��~����)�ɓ_P���ʒu����Ƃ��ł��B
�ȉ��ɂȂ�̂́A�E�}�ŊD�F�ɒ��F��������(�~C���̒��aAB���獶���̔��~����)�ɓ_P���ʒu����Ƃ��ł��B
���̕����̒��ŁA�_O����ł������_��A�ł���A�ł��߂��_�́A����OC�Ɖ~C�Ƃ̌�_D�ł��B
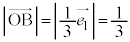 �C
�C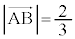 (�~C�̒��a)���A
(�~C�̒��a)���A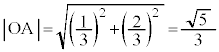
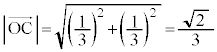 �C
�C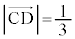 (�~C�̔��a)���A
(�~C�̔��a)���A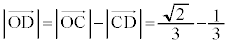
����� �̍ő�l��
�̍ő�l��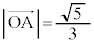 �C�ŏ��l��
�C�ŏ��l��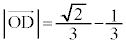 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 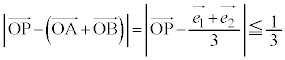 ���AP�́A
���AP�́A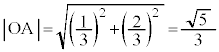
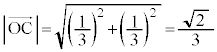 �C
�C