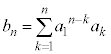大阪大学理系2023年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] nを2以上の自然数とする。
(1) 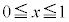 のとき、次の不等式が成り立つことを示せ。
のとき、次の不等式が成り立つことを示せ。 (2) 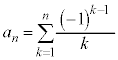 とするとき、次の極限値を求めよ。
とするとき、次の極限値を求めよ。 [解答へ]
[2] 平面上の3点O,A,Bが
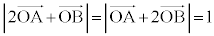 かつ
かつ 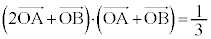
(1) 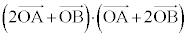 を求めよ。
を求めよ。 (2) 平面上の点Pが
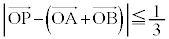 かつ
かつ 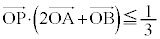
をみたすように動くとき、 の最大値と最小値を求めよ。
の最大値と最小値を求めよ。 [解答へ]
[3] Pを座標平面上の点とし、点Pの座標を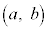 とする。
とする。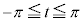 の範囲にある実数t のうち、曲線
の範囲にある実数t のうち、曲線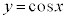 上の点
上の点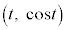 における接線が点Pを通るという条件をみたすものの個数を
における接線が点Pを通るという条件をみたすものの個数を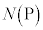 とする。
とする。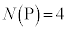 かつ
かつ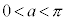 をみたすような点Pの存在範囲を座標平面上に図示せよ。
をみたすような点Pの存在範囲を座標平面上に図示せよ。
[解答へ]
[4] a,bを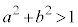 かつ
かつ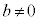 をみたす実数の定数とする。座標空間の点A
をみたす実数の定数とする。座標空間の点A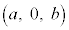 と点P
と点P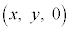 をとる。点O
をとる。点O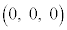 を通り直線APと垂直な平面をαとし、平面αと直線APとの交点をQとする。
を通り直線APと垂直な平面をαとし、平面αと直線APとの交点をQとする。
(1) 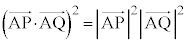 が成り立つことを示せ。
が成り立つことを示せ。 (2) 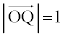 をみたすように点P
をみたすように点P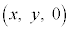 がxy平面上を動くとき、点Pの軌跡を求めよ。
がxy平面上を動くとき、点Pの軌跡を求めよ。 [解答へ]
[5] 1個のさいころをn回投げて、k回目に出た目を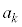 とする。
とする。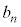 を
を
により定義し、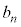 が7の倍数となる確率を
が7の倍数となる確率を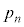 とする。
とする。
(1) 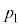 ,
,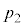 を求めよ。
を求めよ。 (2) 数列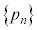 の一般項を求めよ。
の一般項を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 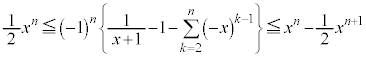
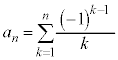 とするとき、次の極限値を求めよ。
とするとき、次の極限値を求めよ。