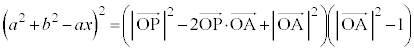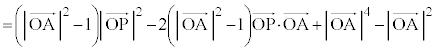��嗝�n���w'23�N�O��[4]
a�Cb��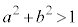 ����
����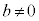 ���݂��������̒萔�Ƃ���B���W��Ԃ̓_A
���݂��������̒萔�Ƃ���B���W��Ԃ̓_A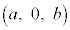 �Ɠ_P
�Ɠ_P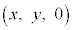 ���Ƃ�B�_O
���Ƃ�B�_O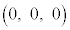 ��ʂ蒼��AP�Ɛ����ȕ��ʂ�α�Ƃ��A����α�ƒ���AP�Ƃ̌�_��Q�Ƃ���B
��ʂ蒼��AP�Ɛ����ȕ��ʂ�α�Ƃ��A����α�ƒ���AP�Ƃ̌�_��Q�Ƃ���B
(1) 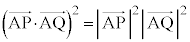 �����藧���Ƃ������B
�����藧���Ƃ������B (2) 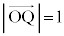 ���݂����悤�ɓ_P
���݂����悤�ɓ_P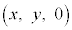 ��xy���ʏ���Ƃ��A�_P�̋O�Ղ����߂�B
��xy���ʏ���Ƃ��A�_P�̋O�Ղ����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�~���ʂʂŐ��2���Ȑ��ɂȂ�A�Ƃ������ł��B���W�ݒ肵�Đ����������v�Z������Ă����Ǝ�ɕ����Ȃ��Ȃ�܂��B(2)��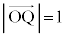 �𗘗p���邽�߂�
�𗘗p���邽�߂�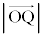 �̌`���c���v�̂悭�v�Z���܂��傤�B
�̌`���c���v�̂悭�v�Z���܂��傤�B
(1) �_Q�́A����AP��̓_�Ȃ̂ŁAk�������Ƃ��āA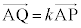 �Ƃ����܂��B
�Ƃ����܂��B ����āA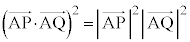 �ł��B
�ł��B
(2) (1)�̌��ʂ�A�CP�̍��W���g���ĕ\���Ƃǂ��Ȃ邩���l���܂��B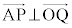 ���A
���A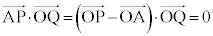 �@��
�@�� 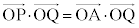 �@����@
�@����@ 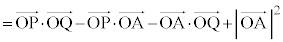
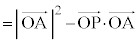 �@(�� �@)
�@(�� �@)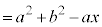 �@(�� �B)�@����C
�@(�� �B)�@����C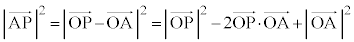 �@����D
�@����D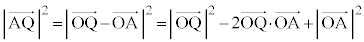
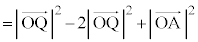 �@(�� �A)
�@(�� �A)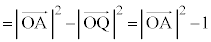
(1)�̌���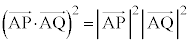 ���A�C�A�D��p���āA
���A�C�A�D��p���āA �B��p���āA
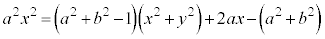 ��
�� 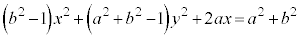
�E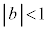 ����
����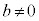 �̂Ƃ��A
�̂Ƃ��A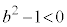 �C
�C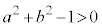 (��蕶)���A�o�Ȑ�
(��蕶)���A�o�Ȑ�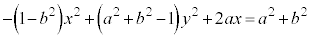
�E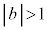 �̂Ƃ��A
�̂Ƃ��A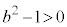 �C
�C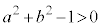 ���A�ȉ~
���A�ȉ~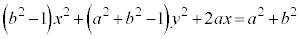 �@......[��]
�@......[��] 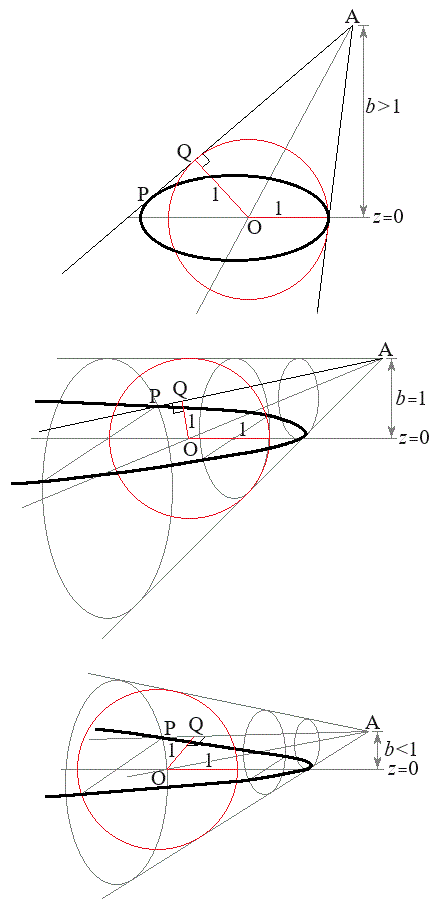 ���D�{��̏�͎��I��(���m�ł͂���܂���)�}������ƁA�E�}�̂悤�ɂȂ�܂��B
���D�{��̏�͎��I��(���m�ł͂���܂���)�}������ƁA�E�}�̂悤�ɂȂ�܂��B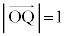 �Ȃ̂�Q�͌��_O�𒆐S�Ƃ��锼�a1�̋���(�Ԑ�)��̓_�ł��BQ��ʂ钼��AP�͂��̋��ʂ̔��aOQ�Ɛ����Ȃ̂ŁAAP�͋��̐ڐ��ł���AP��������AP�̑S�͉̂~���ʂ����܂��B
�Ȃ̂�Q�͌��_O�𒆐S�Ƃ��锼�a1�̋���(�Ԑ�)��̓_�ł��BQ��ʂ钼��AP�͂��̋��ʂ̔��aOQ�Ɛ����Ȃ̂ŁAAP�͋��̐ڐ��ł���AP��������AP�̑S�͉̂~���ʂ����܂��BP�͂��̉~���ʏ�̓_�ł����āAxy����(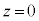 )��̓_�Ȃ̂ŁA(2)�̓��́A�~���ʂ�xy���ʂŐ����Ƃ��̐���ɂł���Ȑ��ł����āA2���Ȑ��ɂȂ�܂��B
)��̓_�Ȃ̂ŁA(2)�̓��́A�~���ʂ�xy���ʂŐ����Ƃ��̐���ɂł���Ȑ��ł����āA2���Ȑ��ɂȂ�܂��B
���̋Ȑ����AA��z���Wb�ɂ���Ăǂ̂悤�ɂȂ邩�A�Ƃ����̂��{��ł��B
�E�}�̂悤�ɁA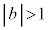 �̂Ƃ��ɂ͑ȉ~�A
�̂Ƃ��ɂ͑ȉ~�A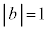 �̂Ƃ��ɂ͕������A
�̂Ƃ��ɂ͕������A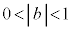 �̂Ƃ��ɂ͑o�Ȑ��ɂȂ�܂��B
�̂Ƃ��ɂ͑o�Ȑ��ɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �C
�C